Índice de Contenidos
En la enseñanza tradicional, las identidades trigonométricas suelen presentarse a los estudiantes como fórmulas a memorizar, sin detenerse en el razonamiento geométrico o histórico que las sustenta. Sin embargo, estas relaciones no surgieron de manera arbitraria: las identidades pitagóricas, de ángulo doble y de ángulo medio tienen un origen común en la interpretación de la circunferencia unitaria y en las demostraciones clásicas basadas en triángulos inscritos. Explorar el génesis de cada identidad —desde la ecuación fundamental \(sin^2 \vartheta + \cos^2 \vartheta =1\), hasta las fórmulas para \(\sin 2\vartheta\) y \(\cos 2\vartheta\), y la deducción de las fórmulas de ángulo medio— no solo clarifica su sentido, sino que convierte el aprendizaje en un proceso lógico de derivación. De este modo, como estudiantes, y también como docentes, podremos generar identidades nuevas a partir de unas pocas relaciones elementales, reduciendo la dependencia de la memorización y fomentando una comprensión más profunda y flexible de su origen y su aplicación.
Círculo Unitario
Consideremos un circulo unitario (radio \(r=1\)), tal como se muestra, parcialmente, en la siguiente figura.
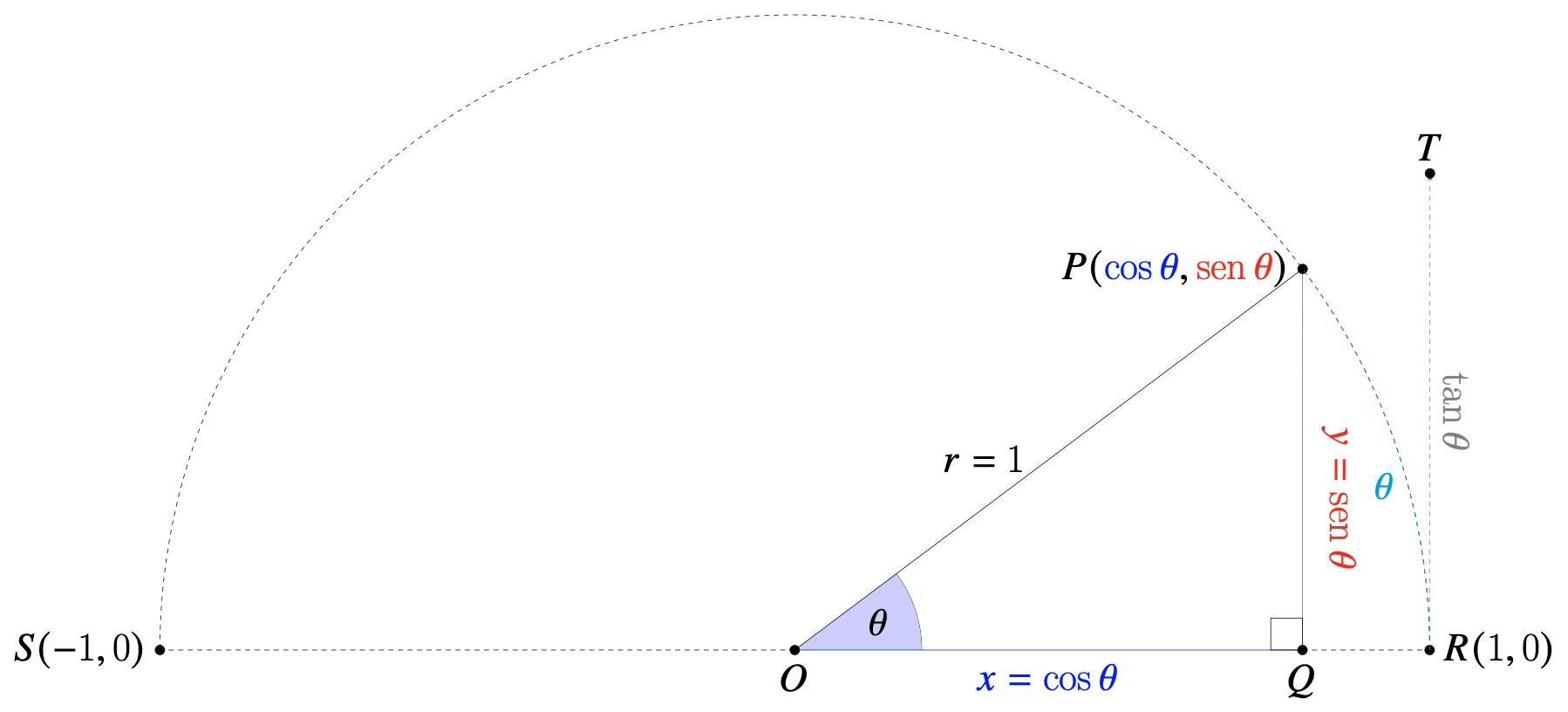
El segmento \(\mathrm{\overline{OP}}\) es un radio del círculo y por lo tanto su magnitud de 1. Se forma un triángulo \(\mathrm{\triangle{OQP}}\), rectángulo en \(\mathrm{Q}\). El punto \(\mathrm{O}\) se encuentra ubicado en el origen (\(O=(0,0)\)).
Podemos sacar las siguientes conclusiones:
\[\begin{alignat}{2} \cos \vartheta = \frac{x}{r} &\implies \cos \vartheta = \frac{x}{1} &\implies \boxed{x = \cos \vartheta} \\[10pt] \sin \vartheta = \frac{y}{r} &\implies \sin \vartheta = \frac{y}{1} &\implies \boxed{y = \sin \vartheta} \end{alignat}\]Es decir, en el círculo unitario, el cateto horizontal (\(x\)) siempre será igual al coseno del ángulo que subtiende con la hipotenusa; y el cateto vertical (\(y\)) siempre será igual al seno del ángulo que subtiende con la hipotenusa.
Identidades Pitagóricas
Consideremos ahora el Teorema de Pitágoras:
\[\begin{equation} a^2 + b^2 = c^2 \end{equation}\]Donde \(a,b\) son las longitudes de los catetos de un triángulo rectángulo y \(c\) la de su hipotenusa.
En el caso del círculo unitario de la figura anterior, nuestros catetos son \(x,y\) y \(r\), respectivamente. Además sabemos que \(r=1\). Luego, podemos redefinir el teorema como:
\[\begin{equation} \begin{split} x^2 + y^2 = 1 \end{split} \end{equation}\]Pero, habíamos establecido que \(x=\cos \vartheta\) y que \(y=\sin \vartheta\), entonces, lo siguiente también es verdad:
\[\begin{equation}\label{eq:pit1} \boxed{\cos^2 \vartheta + \sin^2 \vartheta = 1} \end{equation}\]Basta con despejar la ecuación \(\eqref{eq:pit1}\) para obtener algunas identidades pitagóricas interesantes:
\[\begin{align} \label{eq:pit2} \boxed{\cos^2 \vartheta = 1 - \sin^2 \vartheta} \implies \boxed{\cos \vartheta = \pm \sqrt{1 - \sin^2 \vartheta}} \\[10pt] \label{eq:pit3} \boxed{\sin^2 \vartheta = 1 - \cos^2 \vartheta} \implies \boxed{\sin \vartheta = \pm \sqrt{1 - \cos^2 \vartheta}} \end{align}\]El signo ± depende del cuadrante en el que se encuentre el ángulo \(\vartheta\).
También es posible tomar la ecuación \(\eqref{eq:pit1}\) y dividir ambos lados por \(\sin^2 \vartheta\) o por \(\cos^2 \vartheta\) para producir otras identidades pitagóricas fundamentales.
\[\begin{align} \frac{\cos^2 \vartheta}{\cos^2 \vartheta} + \frac{\sin^2 \vartheta}{\cos^2 \vartheta} = \frac{1}{\cos^2 \vartheta} \implies 1 + \tan^2 \vartheta = \sec^2 \vartheta \\[10pt] \frac{\cos^2 \vartheta}{\sin^2 \vartheta} + \frac{\sin^2 \vartheta}{\sin^2 \vartheta} = \frac{1}{\sin^2 \vartheta} \implies \cot^2 \vartheta + 1 = \csc^2 \vartheta \end{align}\]Así que estas variaciones nos llevan a:
\[\begin{align} \boxed{\sec^2 \vartheta - \tan^2 \vartheta = 1} \\[10pt] \boxed{\csc^2 \vartheta - \cot^2 \vartheta = 1} \end{align}\]Identidades de Suma y Diferencia de Ángulos
Las siguientes dos entidades trigonométricas se utilizan cuando tenemos un ángulo que se presenta como la suma o resta de otros dos. De momento dejaremos estas entidades sin demostración, pues hemos abordado su demostración en artículos separados cuyos enlaces aprecen al final de este artículo.
\[\begin{align} \label{eq:senosm} \boxed{\sin(\vartheta \pm \varphi) = \sin(\vartheta)\cos(\varphi) \pm \cos(\vartheta)\sin(\varphi)}\\[10pt] \label{eq:cosenosm} \boxed{\cos(\vartheta \pm \varphi) = \cos(\vartheta)\cos(\varphi) \mp \sin(\vartheta)\sin(\varphi)} \end{align}\]Es posible combinar \(\eqref{eq:senosm}\) y \(\eqref{eq:cosenosm}\) para obtener una versión para la tangente de la suma o diferencia de dos ángulos. Como se demuestra a continuación:
\[\begin{align} \begin{split} \tan(\vartheta \pm \varphi) = \frac{\sin(\vartheta \pm \varphi)}{\cos(\vartheta \pm \varphi)} = \frac{\sin \vartheta \cos \varphi \pm \cos \vartheta \sin \varphi}{\cos \vartheta \cos \varphi \mp \sin \vartheta \sin \varphi} \\[15pt] \text{Dividir numerador y denominador por } \cos \vartheta \cos \varphi \\[10pt] =\frac{\dfrac{\sin \vartheta \cos \varphi \pm \cos \vartheta \sin \varphi}{\cos \vartheta \cos \varphi}}{\dfrac{\cos \vartheta \cos \varphi \mp \sin \vartheta \sin \varphi}{\cos \vartheta \cos \varphi}} = \frac{\dfrac{\sin \vartheta \cancel{\cos \varphi}}{\cos \vartheta \cancel{\cos \varphi}} \pm \dfrac{\cancel{\cos \vartheta} \sin \varphi}{\cancel{\cos \vartheta} \cos \varphi}}{\dfrac{\cancel{\cos \vartheta \cos \varphi}}{\cancel{\cos \vartheta \cos \varphi}} \mp \dfrac{\sin \vartheta \sin \varphi}{\cos \vartheta \cos \varphi}} = \frac{\dfrac{\sin \vartheta}{\cos \vartheta} \pm \dfrac{\sin \varphi}{\cos \varphi}}{1 \mp \dfrac{\sin \vartheta}{\cos \vartheta} \dfrac{\sin \varphi}{\cos \varphi}} \\[15pt] =\boxed{\frac{\tan \vartheta \pm \tan \varphi}{1 \mp \tan \vartheta \tan \varphi}} \end{split} \end{align}\]Identidades de Ángulo Doble
Otro caso común en trigonometría es cuando tenemos un ángulo que es el doble de otro. A partir de las identidades de suma de ángulos es posible derivar las identidades de ángulo doble.
Seno de un Ángulo Doble
Comencemos con el seno de un ángulo doble:
\[\begin{align} \label{eq:senodoble} \begin{split} \sin(2\vartheta) = \sin(\vartheta + \vartheta) = \sin \vartheta \cos \vartheta + \sin \vartheta \cos \vartheta \\[10pt] = \boxed{2\sin \vartheta \cos \vartheta} \end{split} \end{align}\]De \(\eqref{eq:senodoble}\) se pueden derivar algunas variaciones interesantes. Por ejemplo, podemos considerar que la ecuación es parte un binomio al cuadrado de la forma \(a^2 + 2ab + b^2 = (a+b)^2\):
\[\begin{align} \begin{split} \sin(2\vartheta) = 2\sin \vartheta \cos \vartheta \\ = (\sin^2 \vartheta + 2\sin \vartheta \cos \vartheta + \cos^2 \vartheta) - (\sin^2 \vartheta + \cos^2 \vartheta) \\[10pt] = \boxed{(\sin \vartheta + \cos \vartheta)^2 - 1} \end{split} \end{align}\]Otra ingeniosa variación de la ecuación \(\eqref{eq:senodoble}\) sería la siguiente:
\[\begin{align} \begin{split} \sin(2\vartheta) = 2\sin \vartheta \cos \vartheta \\[10pt] = 2\sin \vartheta \cos \vartheta \cdot \frac{\cos \vartheta}{\cos \vartheta} = \frac{2 \sin \vartheta \cos^2 \vartheta}{\cos \vartheta \cdot 1} = \frac{2 \sin \vartheta \cos^2 \vartheta}{\cos \vartheta \cdot (\sin^2 \vartheta + \cos^2 \vartheta)} \\[10pt] =\frac{2\sin \vartheta}{\cos \vartheta} \cdot \frac{\cos^2 \vartheta}{(\sin^2 \vartheta + \cos^2 \vartheta)} = \frac{2\sin \vartheta}{\cos \vartheta} \div \frac{(\sin^2 \vartheta + \cos^2 \vartheta)}{\cos^2 \vartheta} \\[10pt] =2 \cdot \frac{\sin \vartheta}{\cos \vartheta} \div \left(\frac{\sin^2 \vartheta}{\cos^2 \vartheta} + \frac{\cos^2 \vartheta}{\cos^2 \vartheta}\right) = 2\tan \vartheta \div (\tan^2 \vartheta + 1) \\[10pt] = \boxed{\frac{2 \tan \vartheta}{\tan^2 \vartheta +1}} \end{split} \end{align}\]Coseno de un Ángulo Doble
Pasemos ahora a considerar el caso del coseno de un ángulo doble:
\[\begin{align} \label{eq:cosenodoble} \begin{split} \cos(2\vartheta) = \cos(\vartheta + \vartheta) = \cos \vartheta \cos \vartheta - \sin \vartheta \sin \vartheta \\[10pt] = \boxed{\cos^2 \vartheta - \sin^2 \vartheta} \end{split} \end{align}\]Esta ecuación \(\eqref{eq:cosenodoble}\) también tiene algunas variaciones interesantes. Por ejemplo:
\[\begin{align} \label{eq:cosdoble2} \begin{split} \cos(2\vartheta) = \cos^2 \vartheta - \sin^2 \vartheta = \cos^2 \vartheta - (1-\cos^2 \vartheta) \\[10pt] =\boxed{2\cos^2 \vartheta-1} \end{split} \end{align}\]De forma similar:
\[\begin{align}\label{eq:cosdoble3} \begin{split} \cos(2\vartheta) = \cos^2 \vartheta - \sin^2 \vartheta = (1-\sin^2 \vartheta) - \sin^2 \vartheta \\[10pt] =\boxed{1-2\sin^2 \vartheta} \end{split} \end{align}\]Otra variación de \(\eqref{eq:cosenodoble}\) un poco más elaborada es la siguiente:
\[\begin{align} \begin{split} \cos^2 \vartheta - \sin^2 \vartheta \\[10pt] =(\cos^2 \vartheta - \sin^2 \vartheta) \cdot \frac{\cos^2 \vartheta}{\cos^2 \vartheta} \cdot \frac{1}{1} = \frac{(\cos^2 \vartheta - \sin^2 \vartheta)}{\cos^2 \vartheta} \cdot \frac{\cos^2 \vartheta}{(\cos^2 \vartheta + \sin^2 \vartheta)} \\[10pt] = \frac{(\cos^2 \vartheta - \sin^2 \vartheta)}{\cos^2 \vartheta} \div \frac{(\cos^2 \vartheta + \sin^2 \vartheta)}{\cos^2 \vartheta} = \left[\frac{\cos^2 \vartheta}{\cos^2 \vartheta} - \frac{\sin^2 \vartheta}{\cos^2 \vartheta}\right] \div \left[\frac{\cos^2 \vartheta}{\cos^2 \vartheta} + \frac{\sin^2 \vartheta}{\cos^2 \vartheta}\right]\\[10pt] \left[1-\tan^2 \vartheta\right] \div \left[1+\tan^2 \vartheta\right]\\[10pt] \boxed{\frac{1-\tan^2 \vartheta}{1+\tan^2 \vartheta}} \end{split} \end{align}\]Identidades de Ángulo Medio
En este caso, tenemos un ángulo que es la mitad de otro. Curiosamente, estas identidades se pueden derivar de las de ángulo doble, como se muestra a continuación.
Identidad del Ángulo Medio del Seno
Recordemos que la ecuacion \(\eqref{eq:cosdoble3}\) nos dice que \(\cos(2 \vartheta) = 1-2\sin^2 \vartheta\). Entonces, comencemos haciendo un cambio de variable de la siguiente manera:
\[\varphi = 2 \vartheta \implies \vartheta = \frac{\varphi}{2}\]Luego:
\[\begin{align} \begin{split} \cos(\varphi) = 1-2\sin^2\left(\frac{\varphi}{2}\right) \\[5pt] 2\sin^2\left(\frac{\varphi}{2}\right) = 1-\cos(\varphi) \\[5pt] \sin^2\left(\frac{\varphi}{2}\right) = \frac{1-\cos(\varphi)}{2} \\[10pt] \boxed{\sin\left(\frac{\varphi}{2}\right) = \pm \sqrt{\frac{1-\cos(\varphi)}{2}}} \end{split} \end{align}\]El signo ± depende del cuadrante en el que se encuentre el ángulo \(\frac{\varphi}{2}\).
Identidad del Ángulo Medio del Coseno
Recordemos que la ecuacion \(\eqref{eq:cosdoble2}\) nos dice que \(2\cos^2 \vartheta-1\). Entonces, comencemos haciendo un cambio de variable de la siguiente manera:
\[\varphi = 2 \vartheta \implies \vartheta = \frac{\varphi}{2}\]Luego:
\[\begin{align} \begin{split} \cos(\varphi) = 2\cos^2\left(\frac{\varphi}{2}\right)-1 \\[5pt] 2\cos^2\left(\frac{\varphi}{2}\right) = \cos(\varphi) + 1 \\[5pt] \cos^2\left(\frac{\varphi}{2}\right) = \frac{\cos(\varphi) + 1}{2} \\[10pt] \boxed{\cos\left(\frac{\varphi}{2}\right) = \pm \sqrt{\frac{\cos(\varphi) + 1}{2}}} \end{split} \end{align}\]El signo ± depende del cuadrante en el que se encuentre el ángulo \(\frac{\varphi}{2}\).
Identidad del Ángulo Medio de la Tangente
Claramente, las identidades de tangente se puede derivar de las ecuaciones anteriores, siendo la más obvia la siguiente:
\[\begin{align} \begin{split} \tan\left(\frac{\varphi}{2}\right) = \frac{\sin\left(\frac{\varphi}{2}\right)}{\cos\left(\frac{\varphi}{2}\right)} = \frac{\pm\sqrt{\frac{1-\cos(\varphi)}{2}}}{\pm \sqrt{\frac{\cos(\varphi) + 1}{2}}} \\[10pt] =\boxed{\pm \sqrt{\frac{1-\cos \varphi}{1+\cos \varphi}}} \end{split} \end{align}\]Sin embargo, para el caso de la tangente, hay otras formas más comunes que se puede derivar. Tienen la ventaja de que se deshacen de la raíz cuadrada y que por eso se vuelven muy útiles y sencillas de utilizar.
Esta primera consiste en multiplicar numerador y denominador por \(2\sin\left(\frac{\varphi}{2}\right)\). Veamos:
\[\begin{align} \label{eq:mediotang2} \begin{split} \tan\left(\frac{\varphi}{2}\right) = \frac{\sin\left(\frac{\varphi}{2}\right)}{\cos\left(\frac{\varphi}{2}\right)} \cdot \frac{2\sin\left(\frac{\varphi}{2}\right)}{2\sin\left(\frac{\varphi}{2}\right)} = \frac{2 \sin^2\left(\frac{\varphi}{2}\right)}{2 \cos\left(\frac{\varphi}{2}\right)\sin\left(\frac{\varphi}{2}\right)} \end{split} \end{align}\]Para simplificar esta ecución, primero consideremos la siguiente identidad:
\[\begin{alignat}{3} \label{eq:medioaux1} \begin{split} 2\sin^2 \vartheta = 2(1-\cos^2 \theta) &\qquad \qquad & \text{[Por identidad \eqref{eq:pit3}]} \\ = 2-2\cos^2 \theta \\ = 1 + 1 -2\cos^2 \theta \\ = 1 + (1 -2\cos^2 \theta) \\ = 1 - (2\cos^2 \theta-1) \\[10pt] = \boxed{1-\cos(2\theta)} &\qquad \qquad & \text{[Por identidad \eqref{eq:cosdoble2}]} \end{split} \end{alignat}\]Entonces, usando esta identidad, podemos simplificar nuestra ecuación \(\eqref{eq:mediotang2}\) mediante aplicar un cambio de variable de la siguiente manera:
Sea \(\vartheta = \frac{\varphi}{2}\), luego, podemos continuar con el desarrollo de la ecuación \(\eqref{eq:mediotang2}\) de la siguiete manera:
\[\begin{alignat}{3} \begin{split} \tan \vartheta =\frac{2 \sin^2 \vartheta}{2 \cos \vartheta \sin \vartheta} \\[10pt] = \frac{1-\cos(2\vartheta)}{\sin(2\vartheta)} & \qquad \qquad & \text{[Por identidades \eqref{eq:senodoble} y \eqref{eq:medioaux1}]} \\[10pt] =\frac{1-\cos\left(2 \cdot \frac{\varphi}{2}\right)}{\sin\left(2 \cdot \frac{\varphi}{2}\right)} & \qquad \qquad & \text{[Por inversión del cambio de variable]} \\[10pt] \boxed{\tan \left(\frac{\varphi}{2}\right) = \frac{1-\cos \varphi}{\sin \varphi}} \end{split} \end{alignat}\]Una segunda alternativa es multiplicar el numerador y el denominador de la tange por \(2\cos\left(\frac{\varphi}{2}\right)\), como se muestra a continuación:
\[\begin{equation} \label{eq:mediotang3} \begin{split} \tan\left(\frac{\varphi}{2}\right) = \frac{\sin\left(\frac{\varphi}{2}\right)}{\cos\left(\frac{\varphi}{2}\right)} \cdot \frac{2\cos\left(\frac{\varphi}{2}\right)}{2\cos\left(\frac{\varphi}{2}\right)} = \frac{2\sin\left(\frac{\varphi}{2}\right)\cos\left(\frac{\varphi}{2}\right)}{2\cos^2\left(\frac{\varphi}{2}\right)} \end{split} \end{equation}\]Para simplificar esta ecución, primero consideremos la siguiente identidad:
\[\begin{alignat}{3} \label{eq:medioaux2} \begin{split} 2\cos^2 \vartheta = 2(1-\sin^2 \theta) &\qquad \qquad & \text{[Por identidad \eqref{eq:pit2}]} \\ = 2-2\sin^2 \theta \\ = 1+1 - 2\sin^2 \theta \\ = 1+(1 - 2\sin^2 \theta) \\[10pt] = \boxed{1+\cos(2\theta)} &\qquad \qquad & \text{[Por identidad \eqref{eq:cosdoble3}]} \end{split} \end{alignat}\]Entonces, usando esta identidad, podemos simplificar nuestra ecuación \(\eqref{eq:mediotang3}\) mediante aplicar un cambio de variable de la siguiente manera:
Sea \(\vartheta = \frac{\varphi}{2}\), luego, podemos continuar con el desarrollo de la ecuación \(\eqref{eq:mediotang3}\) de la siguiete manera:
\[\begin{alignat}{3} \begin{split} \tan \vartheta =\frac{2\sin \vartheta \cos \vartheta}{2\cos^2 \vartheta} \\[10pt] = \frac{\sin(2\vartheta)}{1+\cos(2\vartheta)} & \qquad \qquad & \text{[Por identidades \eqref{eq:senodoble} y \eqref{eq:medioaux2}]} \\[10pt] =\frac{\sin\left(2 \cdot \frac{\varphi}{2}\right)}{1+\cos\left(2 \cdot \frac{\varphi}{2}\right)} & \qquad \qquad & \text{[Por inversión del cambio de variable]} \\[10pt] \boxed{\tan\left(\frac{\varphi}{2}\right) = \frac{\sin \varphi}{1-\cos \varphi}} \end{split} \end{alignat}\]Resumen de Identidades
| Identidad | Fórmula |
|---|---|
| Pitagórica fundamental | \(\cos^2\vartheta + \sin^2\vartheta = 1\) |
| Pitagóricas derivadas | \(\sec^2\vartheta - \tan^2\vartheta = 1,\quad \csc^2\vartheta - \cot^2\vartheta = 1\) |
| Suma y diferencia | \(\sin(\vartheta\pm\varphi)=\sin\vartheta\cos\varphi\pm\cos\vartheta\sin\varphi\) |
| \(\cos(\vartheta\pm\varphi)=\cos\vartheta\cos\varphi\mp\sin\vartheta\sin\varphi\) | |
| \(\tan(\vartheta\pm\varphi)=\dfrac{\tan\vartheta\pm\tan\varphi}{1\mp\tan\vartheta\tan\varphi}\) | |
| Ángulo doble | \(\sin2\vartheta = 2\sin\vartheta\cos\vartheta \quad = (\sin \vartheta + \cos \vartheta)^2-1 \quad = \dfrac{2\tan \vartheta}{\tan^2 \vartheta +1}\) |
| \(\cos2\vartheta = \cos^2\vartheta - \sin^2\vartheta \quad = 2\cos^2 \vartheta -1 \quad = 1-2\sin^2 \vartheta \quad = \dfrac{1-\tan^2 \vartheta}{1+\tan^2 \vartheta}\) | |
| Ángulo medio | \(\sin\dfrac{\vartheta}{2} = \pm\sqrt{\dfrac{1-\cos\vartheta}{2}},\quad \cos\dfrac{\vartheta}{2} = \pm\sqrt{\dfrac{1+\cos\vartheta}{2}}\) |
| \(\tan\dfrac{\vartheta}{2} = \dfrac{1-\cos\vartheta}{\sin\vartheta} \quad = \dfrac{\sin \vartheta}{1-\cos \vartheta}\) |