Índice de Contenidos
En la enseñanza tradicional, las identidades trigonométricas suelen presentarse a los estudiantes como fórmulas a memorizar, sin detenerse en el razonamiento geométrico o histórico que las sustenta. Sin embargo, estas relaciones no surgieron de manera arbitraria, más bien tienen un origen común en la interpretación de la circunferencia unitaria y en las demostraciones clásicas basadas en triángulos inscritos. Explorar el génesis de cada identidad no solo clarifica su sentido, sino que convierte el aprendizaje en un proceso lógico de derivación. De este modo, como estudiantes, y también como docentes, podremos generar identidades nuevas a partir de unas pocas relaciones elementales, reduciendo la dependencia de la memorización y fomentando una comprensión más profunda y flexible de su origen y su aplicación.
En este segundo artículo exploraremos dos demostraciones para las identididades trigonométricas de suma y diferencia de dos ángulos.
Suma de Ángulos
En esta sección demostraremos que:
\[\begin{align} \label{eq:senosm} \boxed{\sin(\alpha + \beta) = \sin(\alpha)\cos(\beta) + \cos(\alpha)\sin(\beta)} \end{align}\]Primero, consideremos la siguiente figura en donde se representa la suma de dos ángulos \(\alpha\) y \(\beta\), y algunos triángulos que se derivan de su relación, inscritos en un círculo unitario, del cual solo podemos ver su primer cuadrante.
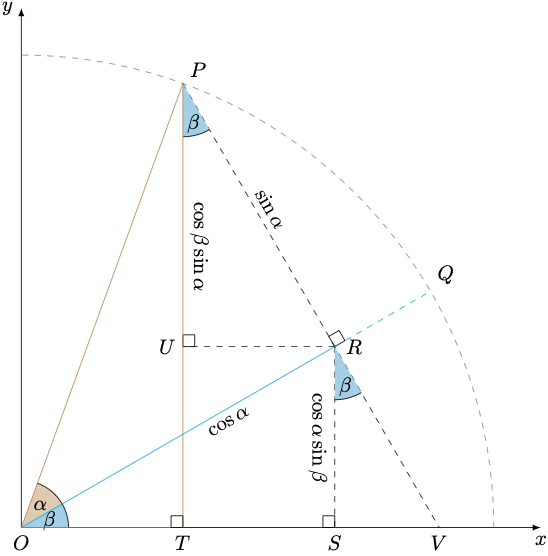
Como se trata de un círculo unitario, los segmentos \(\mathrm{\overline{OP}}\) y \(\mathrm{\overline{OQ}}\) son radios de longitud 1.
Nótese que el ángulo \(\measuredangle{\mathrm{POT}}\) es la suma de \(\alpha + \beta\).
Además, el segmento \(\mathrm{\overline{PR}}\) es perpendicular a \(\mathrm{\overline{OQ}}\) y forma un triángulo \(\triangle{\mathrm{POR}}\), rectángulo en \(\mathrm{R}\) y cuya hipotenusa es el segmento de radio \(\mathrm{\overline{OP}}\).
En \(\triangle{\mathrm{POR}}\) se cumple que:
\[\begin{align}\label{eq:pr} \begin{split} \sin \alpha = \frac{\mathrm{PR}}{\mathrm{OP}} = \frac{\mathrm{PR}}{1} = \mathrm{PR} \\[15pt] \boxed{\mathrm{PR} = \sin \alpha} \end{split} \end{align}\]Además, se cumple que:
\[\begin{align} \label{eq:or} \begin{split} \cos \alpha = \frac{\mathrm{OR}}{\mathrm{OP}} = \frac{\mathrm{OR}}{1} = \mathrm{OR} \\[15pt] \boxed{\mathrm{OR} = \cos \alpha} \end{split} \end{align}\]Seguidamente, en el \(\triangle{\mathrm{ORS}}\) sus ángulos suman \(180^{\circ}\):
\[\begin{align} \begin{split} 90^{\circ} + \beta + \measuredangle{\mathrm{ORS}} = 180^{\circ} \\ \beta + \measuredangle{\mathrm{ORS}} = 180^{\circ}-90^{\circ} \\ \boxed{\measuredangle{\mathrm{ORS}} = 90^{\circ}-\beta} \end{split} \end{align}\]Ahora bien, como \(\mathrm{\overline{PV}}\) es perpendicular a \(\mathrm{\overline{OQ}}\), el ángulo \(\measuredangle{\mathrm{ORV}} = 90^{\circ}\). Luego:
\[\begin{align} \begin{split} \measuredangle{\mathrm{ORV} = \measuredangle{\mathrm{ORS}}} + \measuredangle{\mathrm{SRV}} \\ 90^{\circ} = 90^{\circ}-\beta + \measuredangle{\mathrm{SRV}} \\ 90^{\circ}-90^{\circ}+\beta = \measuredangle{\mathrm{SRV}} \\ \boxed{\measuredangle{\mathrm{SRV}} = \beta} \end{split} \end{align}\]De seguido, podemos afirmar que los ángulos \(\angle{\mathrm{SRV}}\) y \(\angle{\mathrm{UPR}}\) son alternos internos y por lo tanto son congruentes. Así pues, se cumple que:
\[\begin{equation} \measuredangle{UPR} = \measuredangle{SRV} = \beta \end{equation}\]Ahora bien, en \(\triangle{\mathrm{UPR}}\) se cumple que:
\[\begin{alignat}{2} \label{eq:pu} \begin{split} \cos \beta = \frac{\mathrm{PU}}{\mathrm{PR}} = \frac{\mathrm{PU}}{\sin \alpha} & \qquad \qquad & \text{[Según \eqref{eq:pr}]} \\[10pt] \boxed{\mathrm{PU} = \sin \alpha \cos \beta} \end{split} \end{alignat}\]Seguidamente, en el \(\triangle{\mathrm{ORS}}\) se cumple que:
\[\begin{alignat}{2} \begin{split} \sin \beta = \frac{\mathrm{RS}}{\mathrm{OR}} = \frac{\mathrm{RS}}{\cos \alpha} & \qquad \qquad & \text{[Según \eqref{eq:or}]} \\[10pt] \boxed{\mathrm{RS} = \cos \alpha \sin \beta} \end{split} \end{alignat}\]Dado el rectángulo \(\square{\mathrm{TSRU}}\), se cumple que \(\mathrm{RS}=\mathrm{UT}\), por lo tanto:
\[\begin{equation} \label{eq:ut} \mathrm{UT} = \mathrm{RS} = \cos \alpha \sin \beta \end{equation}\]Finalmente, en \(\triangle{\mathrm{POT}}\) se cumple que:
\[\begin{alignat}{2} \begin{split} \sin(\alpha+\beta) = \frac{\mathrm{PT}}{\mathrm{OP}} = \frac{\mathrm{PT}}{\mathrm{1}} = \mathrm{PT}\\[10pt] \sin(\alpha+\beta) = \mathrm{PU} + \mathrm{UT} \\[5pt] \boxed{\sin(\alpha+\beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta} & \qquad & \text{[Según \eqref{eq:pu} y \eqref{eq:ut}]} \\[10pt] \end{split} \end{alignat}\]Diferencia de Ángulos
En esta sección demostraremos que:
\[\begin{align} \label{eq:senodf} \boxed{\sin(\alpha - \beta) = \sin(\alpha)\cos(\beta) - \cos(\alpha)\sin(\beta)} \end{align}\]Primero, consideremos la siguiente figura en donde se representa la diferencia de dos ángulos \(\alpha\) y \(\beta\), y algunos triángulos que se derivan de su relación, inscritos en un círculo unitario, del cual solo podemos ver su primer cuadrante.
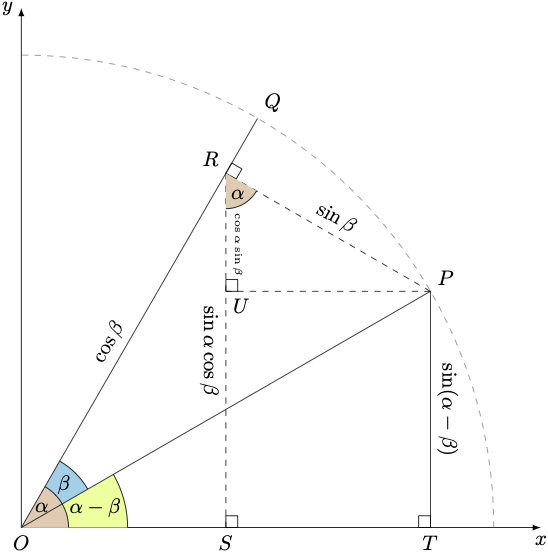
Nótese que los segmentos \(\mathrm{OP}\) y \(\mathrm{OQ}\) son radios de longitud 1.
Según se muestra en la figura 2:
\[\begin{align} \measuredangle{\mathrm{QOT}} &= \alpha \\ \measuredangle{\mathrm{QOP}} &= \beta \\ \measuredangle{\mathrm{POT}} &= \measuredangle{\mathrm{QOT}} - \measuredangle{\mathrm{QOP}} = \alpha - \beta \end{align}\]Con esta información podemos analizar la altura de \(\triangle{\mathrm{POT}}\):
\[\begin{align} \label{eq:pt2} \begin{split} \sin(\alpha-\beta) = \frac{\mathrm{PT}}{\mathrm{OP}} = \frac{\mathrm{PT}}{\mathrm{1}} =\mathrm{PT} \\[10pt] \boxed{\mathrm{PT} = \sin(\alpha-\beta)} \end{split} \end{align}\]Consideremos ahora el segmento \(\overline{\mathrm{PR}}\), que es perpendicular a \(\overline{\mathrm{OQ}}\) en \(\mathrm{R}\) y que forma el triángulo \(\triangle{\mathrm{ORP}}\), rectángulo en en \(\mathrm{R}\) y cuya hipotenusa es \(\mathrm{\overline{OP}}\).
De \(\triangle{\mathrm{ORP}}\) podemos afirmar que:
\[\begin{align} \label{eq:rp2} \begin{split} \sin \beta = \frac{\mathrm{RP}}{\mathrm{OP}} = \frac{\mathrm{RP}}{\mathrm{1}} = \mathrm{RP} \\[10pt] \boxed{\mathrm{RP} = \sin \beta} \end{split} \end{align}\]Además que:
\[\begin{align}\label{eq:or2} \begin{split} \cos \beta = \frac{\mathrm{OR}}{\mathrm{OP}} = \frac{\mathrm{OR}}{\mathrm{1}} = \mathrm{OR} \\[10pt] \boxed{\mathrm{OR} = \cos \beta} \end{split} \end{align}\]Consideremos ahora el segmento \(\mathrm{\overline{RS}}\), perpendicular al eje x en \(\mathrm{S}\) y que forma el triángulo \(\triangle{\mathrm{OSR}}\), rectángulo en \(\mathrm{S}\) y cuya hipotenusa es el segmento \(\mathrm{\overline{OR}}\).
Podemos afirmar lo siguiente de \(\triangle{\mathrm{OSR}}\):
\[\begin{align} \label{eq:rs2} \begin{split} \sin \alpha = \frac{\mathrm{RS}}{\mathrm{OR}} = \frac{\mathrm{RS}}{\cos \beta} & \qquad \text{[Según \eqref{eq:or2}]} \\[10pt] \boxed{\mathrm{RS} = \sin \alpha \cos \beta} \end{split} \end{align}\]Además, como sabemos que la suma de los ángulos de un triángulo es \(180^{\circ}\), se cumple que:
\[\begin{align} \label{eq:sro2} \begin{split} \measuredangle{\mathrm{OSR}} + \measuredangle{\mathrm{ROS}} + \measuredangle{\mathrm{SRO}} = 180^{\circ} \\ 90^{\circ} + \alpha + \measuredangle{\mathrm{SRO}} = 180^{\circ} \\ \alpha + \measuredangle{\mathrm{SRO}} = 180^{\circ} - 90^{\circ} \\ \alpha + \measuredangle{\mathrm{SRO}} = 90^{\circ} \\ \boxed{\measuredangle{\mathrm{SRO}} = 90^{\circ} - \alpha} \end{split} \end{align}\]Seguidamente, podemos determinar la media del ángulo \(\angle{\mathrm{SRP}}\) de la siguiente manera:
\[\begin{align} \label{eq:srp2} \begin{split} \measuredangle{\mathrm{PRO}} = \measuredangle{\mathrm{SRO}} + \measuredangle{\mathrm{SRP}} \\ 90^{\circ} = 90^{\circ} - \alpha + \measuredangle{\mathrm{SRP}} & \qquad \text{[Según \eqref{eq:sro2}]} \\ 90^{\circ} - 90^{\circ} + \alpha = \measuredangle{\mathrm{SRP}} \\ \boxed{\measuredangle{\mathrm{SRP}} = \alpha} \end{split} \end{align}\]Consideremos ahora el segmento \(\mathrm{\overline{PU}}\), perpendicular \(\mathrm{\overline{RS}}\) en \(\mathrm{U}\) y que forma el triángulo \(\triangle{\mathrm{RUP}}\), rectángulo en \(\mathrm{U}\) y cuya hipotenusa es el segmento \(\mathrm{\overline{RP}}\).
Podemos afirmar lo siguiente de \(\triangle{\mathrm{RUP}}\):
\[\begin{align} \label{eq:ru2} \begin{split} \cos \alpha = \frac{\mathrm{RU}}{\mathrm{RP}} = \frac{\mathrm{RU}}{\sin \beta} & \qquad \text{[Según \eqref{eq:rp2}]} \\ \boxed{\mathrm{RU} = \cos \alpha \sin \beta} \end{split} \end{align}\]Finalmente, podemos ver que:
\[\begin{align} \begin{split} \mathrm{PT} = \mathrm{RS} - \mathrm{RU} \\ \sin(\alpha - \beta) = \mathrm{RS} - \mathrm{RU} & \qquad \text{[Según \eqref{eq:pt2}]} \\ \sin(\alpha - \beta) = \sin \alpha \cos \beta - \mathrm{RU} & \qquad \text{[Según \eqref{eq:rs2}]} \\[10pt] \boxed{\sin(\alpha - \beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta} & \qquad \text{[Según \eqref{eq:ru2}]} \\ \end{split} \end{align}\]


