
Índice de Contenidos
Entendiendo los Bloques de Base 10
Los bloques de base 10 son más que simples herramientas para contar; son una manifestación física de todo nuestro sistema numérico, un lenguaje tangible que permite a los jóvenes aprendices ver, tocar y manipular conceptos matemáticos abstractos. Para un niño de primer grado, estos bloques transforman los números de símbolos misteriosos en una página a estructuras concretas y construibles. Antes de comenzar cualquier actividad, es esencial entender las herramientas en sí y los conceptos fundamentales que representan. Esta comprensión inicial es la base sobre la cual se construirá toda la comprensión matemática futura.
Presentando los Bloques
Los bloques de base 10 son materiales manipulativos matemáticos, generalmente hechos de madera, plástico o espuma, que están diseñados para ser proporcionalmente precisos a nuestro sistema numérico de base 10 (Starr, 2023). Para un niño de primer grado, el enfoque se centrará principalmente en dos de los cuatro tipos de bloques estándar:
- La Unidad: Es un cubo pequeño y único, que generalmente mide 1 cm por todos los lados. Representa el valor de 1.
- La Barra: Es un bloque largo y delgado compuesto por diez unidades conectadas en línea. Representa el valor de 10.
Aunque las actividades de primer grado se centrarán en unidades y barras para explorar números hasta 100, es útil conocer los otros bloques para apreciar la escalabilidad del sistema. La placa es un cuadrado formado por 10 barras (o 100 unidades) y representa 100, mientras que el cubo grande está formado por 10 placas (o 1,000 unidades) y representa 1,000 (Hand2mind, 2024).

El verdadero poder de estos bloques reside en sus relaciones físicas y proporcionales. Una barra no es solo un símbolo abstracto para el diez; es físicamente de la misma longitud que diez unidades individuales colocadas una al lado de la otra (Anthony, 2024). Una placa es físicamente del mismo tamaño que diez barras puestas juntas. Esta conexión tangible y visual es lo que hace que los bloques sean profundamente más efectivos para enseñar el valor posicional que las herramientas no proporcionales como los discos de colores, que dependen únicamente de etiquetas y memorización (White Rose Education, 2024). Con los bloques de base 10, a un niño no se le tiene que decir que un diez es más grande que un uno; puede verlo, sentirlo y demostrárselo a sí mismo.
Nomenclatura: “Barra” y “Unidad” vs “Diez” y “Uno”
Un consejo pedagógico crucial es referirse a los bloques por sus formas físicas —”unidad” y “barra”— en lugar de sus valores numéricos —”uno” y “diez” (Starr, 2023). Aunque esto pueda parecer una distinción menor, es una estrategia con visión de futuro que previene una confusión significativa en grados posteriores.
Esta práctica efectivamente “prepara para el futuro” la comprensión matemática de un niño. En los grados superiores de primaria, cuando los estudiantes comienzan a explorar los decimales, los valores de los bloques a menudo se redefinen. Por ejemplo, un maestro podría definir la placa grande como representante del número entero 1. En este contexto, una barra ya no sería un “diez” sino una décima (0.1), y una unidad se convertiría en una centésima (0.01) (Third Space Learning, 2024). Si un niño ha pasado años interiorizando que una barra es siempre un “diez”, se enfrenta al obstáculo cognitivo innecesario de desaprender esta definición fija (Starr, 2023). Al usar consistentemente los nombres “unidad”, “barra” y “placa”, el enfoque permanece en la relación entre los bloques (es decir, siempre se necesitan diez de uno para hacer el siguiente tamaño), que es el concepto central del sistema de base 10. Esto permite que los valores sean flexibles y se adapten a nuevos contextos matemáticos sin causar confusión.
El Concepto de Unitización
Antes de que un niño pueda usar eficazmente los bloques de base 10 para cualquier operación matemática, primero debe comprender un concepto conocido como “unitización” (Starr, 2023). En términos simples, unitizar es la capacidad de ver un grupo de objetos como una sola entidad mientras se comprende simultáneamente que está compuesto de unidades individuales (Math Transformations, 2024). Una barra de diez es el ejemplo por excelencia de este concepto: es una cosa (una barra) y diez cosas (diez unidades) al mismo tiempo.
Este concepto es el prerrequisito más importante para usar los bloques de base 10. Un niño que aún no ha desarrollado la capacidad de unitizar mirará una colección de tres barras y dos unidades y las contará como cinco objetos individuales (“uno, dos, tres, cuatro, cinco”) en lugar de reconocer su valor como treinta y dos (Starr, 2023). Este malentendido fundamental hace imposible construir números correctamente o realizar operaciones como la suma y la resta.
Para determinar si un niño está listo para trabajar con bloques de base 10, se puede observar cómo aborda el conteo. Cuando se le presenta una pila de objetos pequeños, ¿los agrupa en montones de cinco o diez para contar de manera más eficiente, o cuenta cada artículo uno por uno? La capacidad de ver y usar grupos es un claro indicador de la preparación para unitizar (Starr, 2023).
De lo Concreto a lo Abstracto
El primer grado es un período especial de desarrollo cognitivo donde los niños comienzan su viaje desde el pensamiento puramente concreto hacia un razonamiento más abstracto (Happy Numbers, 2024). El concepto de unitización no es simplemente una habilidad matemática; representa el puente cognitivo que facilita este salto monumental. Cuando un niño mira una barra física y comprende su doble naturaleza —como un grupo de diez— está participando en uno de sus primeros actos verdaderos de pensamiento matemático abstracto. Está manteniendo dos ideas distintas pero relacionadas sobre un solo objeto en su mente. Esta habilidad es la base del valor posicional, que a su vez es la base de todo nuestro sistema numérico.
La falta de construcción de este puente cognitivo es una de las principales causas de dificultades posteriores con las operaciones de varios dígitos. Un niño que no puede unitizar permanece atado al proceso lento, laborioso e ineficiente de contar todo de uno en uno. Puede que aprenda a seguir los pasos de un algoritmo, pero carecerá del sentido numérico subyacente para entender por qué funciona o para resolver problemas de manera flexible. Al asegurar una sólida comprensión de la unitización antes de avanzar, se le proporciona al niño la herramienta mental esencial necesaria para construir una comprensión profunda y duradera de las matemáticas.
Valor Posicional y Sentido Numérico
Una vez que el niño comprende la naturaleza de los bloques y el concepto de unitización, la verdadera construcción puede comenzar. Esta sección detalla actividades creativas y prácticas diseñadas para construir una comprensión robusta y flexible del valor posicional y el sentido numérico para números hasta 100. Estas actividades no se tratan solo de obtener la respuesta correcta; se tratan de internalizar la estructura de los números.
Componiendo Números
La actividad más fundamental con los bloques de base 10 es traducir un número escrito en una estructura física. Este proceso, conocido como componer un número, crea un vínculo directo e inolvidable entre el símbolo abstracto y su cantidad concreta.
La actividad se realiza mejor utilizando un simple tapete de valor posicional, que puede ser una hoja de papel con una línea en el medio, creando dos columnas etiquetadas como “Decenas” y “Unidades” (White Rose Education, 2024). Para construir el número 34, por ejemplo, el niño colocaría tres barras en la columna de “Decenas” y cuatro unidades en la columna de “Unidades” (Good Neighbors Math, 2024). Mientras lo hace, se le debe animar a contar en voz alta, primero contando de diez en diez para las barras (“10, 20, 30”) y luego continuando de uno en uno para las unidades (“31, 32, 33, 34”) (Good Neighbors Math, 2024). Este simple acto refuerza el valor de la posición de cada dígito y solidifica la comprensión de que el ‘3’ en 34 no es solo un tres, sino tres grupos de diez.
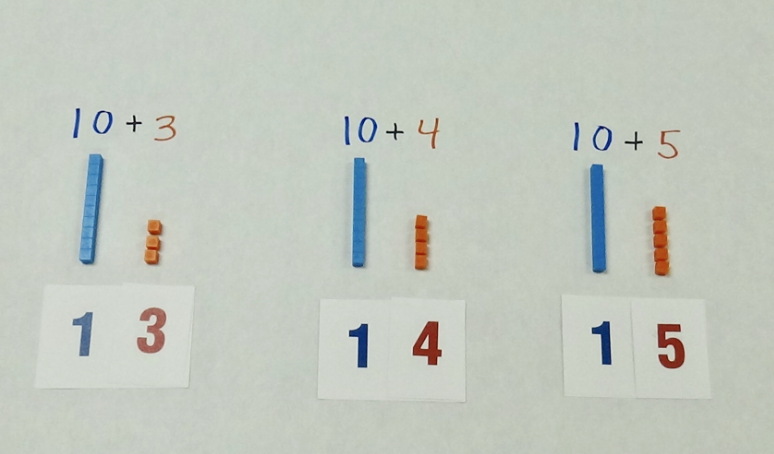
Comparando Números
La comparación de números puede transformarse de un ejercicio de hoja de trabajo rutinario en una competencia emocionante. Esta actividad refuerza visual y experimentalmente la regla más importante de la comparación de números: el valor de la posición de las decenas es siempre más significativo que el valor de la posición de las unidades.
Una forma atractiva de practicar esto es a través de un juego llamado “Guerra de Base Diez” (ActiLearn, 2024). Usando una baraja de cartas con números del 1 al 99, dos jugadores sacan una carta cada uno y construyen el número con sus bloques. A la cuenta de tres, revelan sus creaciones. La regla para determinar el ganador es fundamental: los jugadores siempre deben comparar primero el número de barras (decenas) (Hand2mind, 2024). Por ejemplo, si un jugador construye 42 (4 barras, 2 unidades) y el otro construye 28 (2 barras, 8 unidades), el jugador con 42 gana inmediatamente porque cuatro barras son más que dos barras. Las ocho unidades, a pesar de ser una cantidad mayor que dos unidades, son irrelevantes porque su valor total es menor que el de una sola barra. Solo si el número de barras es el mismo, los jugadores proceden a comparar el número de unidades para encontrar al ganador (ActiLearn, 2024). Este juego convierte el concepto abstracto de la jerarquía del valor posicional en una regla de juego tangible y memorable.

Números Flexibles
Una de las concepciones erróneas más comunes y persistentes en las matemáticas tempranas es la creencia de que un número solo puede representarse de una manera estándar (por ejemplo, 35 es solo 3 decenas y 5 unidades) (Milwaukee Public Schools, 2024). La actividad “¿De Cuántas Maneras?” está diseñada específicamente para desmantelar este pensamiento rígido y construir una comprensión flexible de los números, que es la base conceptual para la reagrupación en la resta.
La actividad comienza presentando un número en su forma estándar. Por ejemplo, construir el número 35 usando 3 barras y 5 unidades. Luego, se plantea el desafío: “¿Cómo podemos mostrar el número 35 de una manera diferente, usando una combinación diferente de bloques?” (Gray, 2024). Guía al niño para que realice un canje. Puede tomar una de las barras e intercambiarla por 10 unidades sueltas. Ahora, tiene 2 barras y 15 unidades. Se ve diferente, y el número total de bloques físicos ha cambiado, pero es crucial contar el valor y confirmar que sigue siendo 35. Este proceso puede repetirse hasta que el número se represente completamente por unidades (1 barra y 25 unidades, y finalmente 35 unidades) (Third Space Learning, 2024). Celebrar cada nuevo descubrimiento refuerza la idea de que los números son cantidades flexibles, no recetas fijas.
Descomposición para la Reagrupación
La capacidad de representar números de múltiples maneras equivalentes no es simplemente una curiosidad intelectual; es el prerrequisito cognitivo directo para comprender la resta con reagrupación. El algoritmo abstracto de “pedir prestado” de la posición de las decenas a menudo parece una regla misteriosa y arbitraria para un niño que solo ha practicado la representación del número 35 en su forma estándar de 3 decenas y 5 unidades (Mighty Owl, 2024). Cuando se enfrenta a un problema como 35 - 7, se queda conceptualmente atascado.
Sin embargo, para un niño que ha participado físicamente en la actividad “¿De Cuántas Maneras?”, la situación es completamente diferente. Tiene una comprensión profunda y experiencial de que el número 35 también es 2 decenas y 15 unidades. Para este niño, el acto de reagrupar en la resta no es una nueva regla que deba memorizar. Es una elección intuitiva y lógica. Reconoce que la representación estándar de 35 no es útil para quitar 7 unidades, por lo que simplemente elige una representación más útil del mismo número para resolver el problema. Dominar esta descomposición flexible antes de introducir el algoritmo formal de la resta transforma un concepto abstracto difícil en una decisión simple y práctica. Es la diferencia entre seguir ciegamente una receta y entender verdaderamente cómo cocinar.
Suma con Bloques
La suma es el proceso de combinar y construir. Al enmarcar este proceso dentro de historias y juegos, el algoritmo abstracto para la reagrupación (a menudo llamado “llevarse una”) se convierte en una acción concreta, lógica y comprensible. Esta sección proporciona una guía paso a paso para enseñar la suma, pasando de la manipulación práctica a la representación abstracta.
Suma Narrativa
Cada problema matemático puede ser una historia. En lugar de presentar una ecuación desnuda como 24 + 13, enmárcala dentro de una narrativa simple para aumentar el compromiso y proporcionar contexto. Por ejemplo: “Nuestra ciudad de bloques tiene 24 residentes (representados por 2 barras y 4 unidades). Llega un nuevo autobús que trae 13 residentes más (1 barra y 3 unidades). ¿Cuántas personas viven ahora en nuestra ciudad?” (Saddle Up for 2nd Grade, 2024). El niño luego combina los bloques para encontrar el total. Este enfoque conecta las operaciones matemáticas con escenarios del mundo real, haciendo el proceso más significativo y memorable.
Reagrupación: El “Canje hacia Arriba”
Enseñar la suma con reagrupación es uno de los pasos más críticos en las matemáticas de primer grado. El juego del “Canje hacia Arriba” transforma este proceso potencialmente confuso en un juego simple con una regla clara. Usemos el problema de ejemplo 28 + 34.
Paso 1: Construir Ambos Números. En un tapete de valor posicional, el niño construye ambos sumandos. Para 28 + 34, colocaría 2 barras y 8 unidades para el primer número, y 3 barras y 4 unidades para el segundo número (Techie Turtle Teacher, 2024).
Paso 2: Combinar las Unidades Primero. La regla cardinal de las operaciones de varios dígitos es comenzar siempre por la posición de las unidades. El niño mueve físicamente todos los bloques de unidades a un solo grupo. En este caso, 8 unidades más 4 unidades equivalen a 12 unidades.
Paso 3: Hacer Cumplir la “Regla del Canje”. Introduce la única y simple regla del juego: “¡La ‘Casa de las Unidades’ tiene una regla: no puedes tener 10 o más unidades viviendo allí! Si las tienes, ¡tienes que canjear hacia arriba!”. Guía al niño para que cuente un grupo de 10 unidades de su pila de 12. Estas 10 unidades se intercambian físicamente por una nueva barra (Happy Numbers, 2024).
Paso 4: Mover la Nueva Barra. Esta nueva barra, que representa las unidades canjeadas, se mueve a la “Casa de las Decenas” (la columna de las decenas) (ASCD Professional Development Online, 2024). Este movimiento físico es la representación concreta de la suma con “llevadas”.
Paso 5: Encontrar el Total. Ahora, el niño cuenta las unidades restantes (2) y luego cuenta todas las barras en la columna de las decenas (las 2 originales, las 3 originales y la 1 nueva barra del canje). El conteo final es de 6 barras y 2 unidades, revelando la respuesta: 62.
La Vía Concreto-Pictórico-Abstracta
El siguiente paso crucial es transferir esta comprensión práctica al trabajo con papel y lápiz. Esto se hace mejor a través de un proceso gradual conocido como la vía Concreto-Pictórico-Abstracta (CPA) (Techie Turtle Teacher, 2024).
Etapa Pictórica: Después de dominar el proceso con bloques físicos, el niño pasa a dibujarlos. Para resolver 28 + 34, dibujaría los bloques para ambos números. Para mostrar la reagrupación, dibuja un círculo alrededor de un grupo de 10 unidades, dibuja una ‘X’ grande a través del círculo para mostrar que han sido “canjeadas”, y luego dibuja una nueva barra en la columna de las decenas (Techie Turtle Teacher, 2024).
Etapa Pictórica Simplificada (Cuadrados, Palos y Puntos): A medida que adquieren más confianza, pueden pasar a un método abreviado más rápido y abstracto. En lugar de dibujos detallados, representan las centenas con cuadrados, las decenas con palos (o líneas) y las unidades con puntos (Techie Turtle Teacher, 2024). Este método es más rápido que dibujar bloques detallados pero aún mantiene la agrupación visual crucial del valor posicional, sirviendo como un puente poderoso hacia el algoritmo final, puramente abstracto.
Previniendo Errores con Movimiento Físico
El acto físico de trabajar con bloques de base 10 proporciona una poderosa memoria cinestésica que puede prevenir directamente errores comunes que surgen cuando los estudiantes aprenden el algoritmo abstracto sin una base conceptual. Un error frecuente identificado en la investigación ocurre cuando un estudiante, al resolver 28 + 34, calcula correctamente que 8 + 4 = 12 y escribe “11”. Luego, calcula 2 + 3 = 5 y escribe “5”. Está tratando las dos columnas como problemas completamente separados y no tiene comprensión del valor del “uno” que se lleva (ASCD Professional Development Online, 2024).
El juego del “Canje hacia Arriba” hace que este error sea conceptualmente imposible. El niño experimenta físicamente las 10 unidades desapareciendo de la columna de las unidades y reapareciendo como una sola barra nueva en la columna de las decenas (ASCD Professional Development Online, 2024). Esta acción construye una comprensión profunda y no verbal de que el “1” en “12” no representa una unidad; representa un grupo de diez, y su lugar apropiado es con las otras decenas. Este proceso físico de canjear y mover es lo que da verdadero significado a la instrucción abstracta de “llevarse la una”, transformándola de un truco mágico a un procedimiento lógico.
Resta con Bloques
La resta, particularmente con reagrupación (a menudo llamada “pedir prestado”), puede ser uno de los conceptos más desafiantes para los niños de primer grado. El proceso a menudo parece contraintuitivo y está lleno de oportunidades para cometer errores. El uso de bloques de base 10 desmitifica este proceso, transformando la idea abstracta y a menudo confusa de “pedir prestado” en un “canje hacia abajo” lógico, tangible e intuitivo.
Regla de Oro: Solo el Primer Número
Antes de comenzar cualquier problema de resta, es vital establecer una regla inquebrantable: al modelar la resta, solo se construye el primer número (el minuendo) (ASCD Professional Development Online, 2024). Para el problema 42 - 15, el niño solo debe construir el número 42 con sus bloques. El segundo número, 15, representa la cantidad que se quitará físicamente de la cantidad inicial. Una fuente común de profunda confusión para los jóvenes aprendices es construir ambos números y luego tratar de averiguar qué hacer con las dos pilas separadas (ASCD Professional Development Online, 2024). Hacer cumplir esta regla de “construir solo el primer número” desde el principio elimina esta confusión y prepara el escenario para una comprensión clara del proceso de resta.
El “Canje hacia Abajo”
El método del “Canje hacia Abajo” proporciona un enfoque paso a paso y basado en una historia para la resta con reagrupación que es a la vez concreto y fácil de seguir. Usemos el problema de ejemplo 42 - 15.
Paso 1: Construir el Minuendo. El niño comienza construyendo el número 42 en su tapete de valor posicional, colocando 4 barras y 2 unidades.
Paso 2: Empezar con las Unidades. Al igual que con la suma, todas las operaciones comienzan en la posición de las unidades. El problema requiere quitar 5 unidades. El niño mira su tapete e inmediatamente se enfrenta al dilema central de la reagrupación: “Necesitamos quitar 5 unidades, pero solo tenemos 2. ¡No tenemos suficientes!” (Mighty Owl, 2024). Esto crea un problema claro y comprensible que necesita una solución.
Paso 3: El “Canje hacia Abajo”. La solución se enmarca como una transacción simple: “Necesitamos más unidades. ¡Vamos a la ‘Casa de las Decenas’ de al lado y hagamos un canje!”. El niño toma físicamente una barra de la columna de las decenas y la intercambia por 10 unidades sueltas (Starr, 2023). Estas 10 nuevas unidades se colocan en la columna de las unidades. El niño ahora tiene 3 barras y 12 unidades en su tapete. Es crucial en esta etapa hacer una pausa y enfatizar que el valor total de los bloques sigue siendo 42, solo que representado de una manera diferente y más útil.
Paso 4: Completar la Resta. Ahora que hay suficientes unidades, el proceso es sencillo. El niño quita 5 unidades de las 12 unidades, dejando 7. Luego, se mueve a la columna de las decenas y quita 1 barra de las 3 barras restantes, dejando 2. Los bloques que quedan en el tapete —2 barras y 7 unidades— muestran claramente la respuesta: 27.
CPA en la Resta
Al igual que con la suma, la transición de los bloques concretos al algoritmo abstracto se gestiona mejor a través de la vía CPA.
Etapa Pictórica: El niño comienza dibujando los bloques para el primer número (por ejemplo, 4 barras y 2 puntos para 42). Para mostrar la reagrupación, tacha una de las barras y luego dibuja 10 nuevos puntos en la columna de las unidades. Finalmente, tacha los bloques que se están restando (1 barra y 5 puntos) para encontrar la respuesta (ASCD Professional Development Online, 2024).
Etapa Pictórica Simplificada: Progresa al método abreviado de “palos y puntos”, siguiendo el mismo proceso de dibujar el número inicial, tachar un palo para reagrupar, dibujar 10 nuevos puntos y luego tachar el sustraendo para encontrar la diferencia (ASCD Professional Development Online, 2024). Esta etapa proporciona un análogo visual claro al tachado y reescritura de números en el algoritmo estándar.
Más Allá de “Pedir Prestado”
El término tradicional “pedir prestado” es conceptualmente engañoso y puede crear una confusión innecesaria para los jóvenes aprendices. La palabra “pedir prestado” implica que el artículo tomado debe ser devuelto eventualmente, lo cual no es lo que sucede en el algoritmo de la resta (Mighty Owl, 2024). Esta imprecisión lingüística puede dificultar la capacidad de un niño para formar un modelo mental correcto del proceso.
La acción física con los bloques revela una forma más precisa de pensar y hablar sobre la reagrupación. El proceso no es un préstamo; es un canje justo o un intercambio. Una barra de diez se desarma en sus unidades constituyentes (Starr, 2023). Por lo tanto, se recomienda encarecidamente reemplazar el lenguaje de “pedir prestado” con verbos activos y concretos que describan con precisión la acción que se está realizando. Frases como:
- “Vamos a canjear una decena por diez unidades.”
- “Necesitamos desarmar una decena.”
- “Vamos a intercambiar esta barra por algunas unidades.”
Usar este lenguaje más preciso y descriptivo ayuda al niño a construir una base conceptual más fuerte y precisa. Alinea su monólogo interno con la realidad física de la manipulación, haciendo que todo el proceso de reagrupación se sienta lógico e intuitivo en lugar de una regla mágica o arbitraria.
Creatividad y Razonamiento Espacial
Los bloques de base 10 no son solo herramientas para la aritmética; también son instrumentos poderosos para fomentar la creatividad, las habilidades de ingeniería y el razonamiento espacial. Al integrarlos en actividades STEAM (Ciencia, Tecnología, Ingeniería, Artes y Matemáticas), se puede demostrar que las matemáticas no son una materia aislada, sino un lenguaje interconectado que se utiliza para describir, diseñar y crear en el mundo físico. Estas actividades ayudan a desarrollar habilidades cruciales de visualización espacial que son fundamentales para el éxito posterior en geometría, física y diseño (The Institute for Arts Integration, 2024).
Arquitectura de Base 10
Esta actividad abierta, inspirada en el concepto de “Edificios de Base Diez”, desata la imaginación de un niño mientras refuerza simultáneamente su sentido numérico y su comprensión del valor posicional (The Institute for Arts Integration, 2024). La actividad puede estructurarse con desafíos crecientes.
Desafío 1: Construcción Libre. Se le da al niño una colección de bloques y la simple instrucción de construir lo que quiera: un castillo, una nave espacial, un animal o incluso su nombre escrito con bloques (Gray, 2024). No hay reglas, y la creatividad es el objetivo principal. Una vez terminada la creación, entra en juego el componente matemático: el niño debe contar cuidadosamente las barras y unidades utilizadas para calcular el valor numérico total de su obra maestra.
Desafío 2: Construcción con Valor Objetivo. El desafío se invierte. El adulto proporciona un número objetivo específico y un tema: “¿Puedes construirme un robot que tenga un valor de exactamente 63?” o “Diseña una casa con un valor de 48”. Esta tarea requiere planificación y un conteo cuidadoso. Curiosamente, la creación de cada niño se verá completamente diferente, pero todas tendrán el mismo valor numérico, ilustrando poderosamente que un solo número puede tener muchas representaciones físicas diferentes.
Desafío 3: Construcción con Restricciones. Esta versión avanzada del desafío introduce una restricción que obliga al pensamiento flexible y a la reagrupación. Por ejemplo: “Construye una estructura con un valor de 124, pero solo se te permite usar un máximo de ocho barras” (Gray, 2024). Para lograr esto, el niño no puede simplemente representar 124 de la manera estándar (1 placa, 2 barras, 4 unidades). Se verá obligado a canjear la placa por diez barras, y luego canjear algunas de esas barras por unidades para cumplir con la restricción, profundizando su comprensión de la composición de los números.
De 3D a 2D
Para profundizar la conexión entre el arte y las matemáticas, la actividad puede extenderse haciendo que el niño dibuje su creación tridimensional en una hoja de papel bidimensional (The Institute for Arts Integration, 2024). Este ejercicio cierra la brecha entre la conciencia espacial 3D y la representación 2D, una habilidad fundamental en campos que van desde la arquitectura y la ingeniería hasta el diseño gráfico. Luego pueden agregar color y detalles a su boceto, convirtiendo su estructura de bloques en una obra de arte completa.
Mosaicos y Patrones
Aunque los bloques de base 10 no son lo mismo que los bloques de patrones tradicionales, sus formas geométricas —cuadrados (el extremo de una unidad) y rectángulos (la cara de una barra)— se pueden usar para crear hermosos mosaicos y patrones 2D en una superficie plana. Esto proporciona una excelente oportunidad para introducir el concepto geométrico de simetría de una manera práctica. Un adulto puede crear la mitad de un diseño simétrico y luego desafiar al niño a construir la imagen especular perfecta en el otro lado de una línea de simetría (por ejemplo, un trozo de hilo o una línea dibujada) (ActiLearn, 2024). Esta actividad lúdica introduce ideas geométricas sofisticadas en un formato accesible y atractivo.
Matemáticas del Mundo Físico
Estas actividades de construcción creativa enseñan una lección profunda y de orden superior que trasciende la simple aritmética. Demuestran que las matemáticas no son solo una materia abstracta confinada a las aulas y las hojas de trabajo, sino un lenguaje poderoso y esencial utilizado para describir, cuantificar y crear en el mundo físico. Cuando un niño construye un “robot con un valor de 63”, está forjando un vínculo inquebrantable entre un número abstracto y un objeto tangible y físico que él mismo diseñó y construyó.
Esta experiencia les ayuda a internalizar que los números tienen forma, volumen y estructura. Sienta una base intuitiva para conceptos posteriores y más formales en geometría, como el área y el volumen, e incluso en física e ingeniería (The Institute for Arts Integration, 2024). Este enfoque transforma las matemáticas de un conjunto de reglas arbitrarias que deben memorizarse en una herramienta dinámica para la creatividad, la resolución de problemas y la comprensión del mundo que les rodea. Responde a la perenne pregunta infantil, “¿Cuándo usaré esto alguna vez?”, mostrándoles que lo están usando ahora mismo, de la manera más creativa y alegre posible.
Juegos y Actividades Lúdicas
Para construir una verdadera fluidez matemática, la práctica es esencial. Sin embargo, la práctica no tiene por qué ser monótona. Los juegos son una herramienta poderosa para reforzar conceptos en un entorno de bajo estrés y alto compromiso. Esta sección proporciona un manual de juegos y actividades cortas que se pueden usar repetidamente para desarrollar la fluidez en el valor posicional y las operaciones, y para explorar nuevas fronteras matemáticas como la estimación y la medición.
Catálogo de Juegos
Los siguientes juegos son fáciles de aprender, requieren materiales mínimos y proporcionan práctica específica para habilidades clave de primer grado.
| Nombre del Juego | Concepto Central Enseñado | Materiales Necesarios | Cómo Jugar (Breve) | Giro Creativo |
|---|---|---|---|---|
| Carrera a 100 (Gray, 2024) | Valor Posicional, Suma, Reagrupación | Bloques de base 10, 1-2 dados, tapete de valor posicional | Los jugadores se turnan para lanzar los dados, agregar esa cantidad de unidades a su tapete y canjear 10 unidades por una barra siempre que sea posible. El primer jugador en adquirir 10 barras (un valor de 100) gana. | Juega “Carrera desde 100”: Comienza con 10 barras, lanza los dados y resta esa cantidad, practicando la resta y la reagrupación. El primero en llegar a cero gana. |
| Guerra de Base Diez (ActiLearn, 2024) | Comparación de Números, Valor Posicional | Bloques de base 10, tarjetas de números (1-99) | Cada jugador saca una carta, construye el número con bloques y comparan. El jugador con el valor mayor gana ambas cartas. El jugador con más cartas al final gana. | Para un desafío, juega con tres jugadores. El jugador con el valor mayor gana la ronda, y también debe ordenar correctamente los tres números de menor a mayor. |
| BINGO de Base Diez (ActiLearn, 2024) | Reconocimiento de Números, Valor Posicional | Cartones de BINGO con números, tarjetas de llamada con imágenes de bloques de base 10 | El que llama muestra una tarjeta con una imagen de bloques (por ejemplo, 4 barras y 7 unidades). Los jugadores calculan el valor (47) y cubren ese número en su cartón de BINGO si lo tienen. | Deja que el niño sea el “llamador”. Esto requiere que practique contar los bloques y comunicar claramente el número, reforzando los conceptos desde una perspectiva diferente. |
| Adivina Mi Número (ActiLearn, 2024) | Valor Posicional, Razonamiento Lógico, Vocabulario Numérico | Bloques de base 10, un libro o pantalla para ocultar los bloques | Un jugador construye un número secreto de dos dígitos y lo oculta. El otro jugador hace preguntas de sí/no para deducir el número (por ejemplo, “¿Tiene más de 4 decenas?” “¿El número de unidades es un número par?”). | Para aumentar el desafío, limita el número de preguntas permitidas (por ejemplo, cinco preguntas). Esto fomenta preguntas más estratégicas y eficientes. |
| La Tienda de Base 10 (ActiLearn, 2024) | Resta, Dar el Cambio, Educación Financiera | Juguetes pequeños u objetos con etiquetas de precio hechas de imágenes de bloques de base 10, una “cartera” de bloques | El niño actúa como el comprador, usando su cartera de bloques para “comprar” artículos de la tienda. Debe pagar la cantidad exacta o calcular el “cambio” que debería recibir. | Introduce precios de “oferta”. Un artículo con un precio original de 35 (3 barras, 5 unidades) ahora cuesta “10 menos”. El niño debe primero calcular el nuevo precio y luego realizar la compra. |
Estimación y Medición
Los bloques de base 10 también se pueden usar para introducir otros conceptos matemáticos importantes más allá de la aritmética.
Estimación: La capacidad de hacer una suposición razonable es una habilidad vital y una piedra angular del sentido numérico. Un juego simple y divertido es “¿Cuántos Puedes Sostener?” (The Institute for Arts Integration, 2024). Haz que el niño tome un gran puñado de cubos unitarios. Antes de contar, pídele que estime cuántos cree que tiene. Registra su suposición. Luego, haz que cuente cuidadosamente los cubos (quizás haciendo grupos de diez) para encontrar el número real. Comparar la estimación con el conteo real ayuda a refinar sus habilidades de estimación con el tiempo.
Medición No Estándar: Antes de que los niños aprendan sobre unidades estándar como pulgadas o centímetros, aprenden el concepto fundamental de la medición utilizando unidades no estándar. Los bloques de base 10 son perfectos para esto. Los cubos unitarios y las barras se pueden usar como unidades de medida consistentes (Starr, 2023). Plantea preguntas como, “¿Cuántas unidades azules de largo es tu libro favorito?” o “¿Cuántas barras amarillas de alto es tu silla?”. Esta actividad enseña el proceso de medición: alinear las unidades de extremo a extremo sin espacios y contar cuántas unidades se necesitan para igualar la longitud de un objeto.
Juegos como Evaluación
Aunque los juegos son inherentemente divertidos, también cumplen un propósito pedagógico crítico: son una forma de evaluación auténtica. Una hoja de trabajo a menudo puede evaluar si un niño ha memorizado un procedimiento, pero puede no revelar su verdadera comprensión conceptual. La forma en que un niño juega un juego, sin embargo, proporciona una ventana directa y reveladora a su proceso de pensamiento (Third Space Learning, 2024).
Por ejemplo, durante un juego de “Carrera a 100”, observa al niño de cerca cuando su columna de unidades tiene más de diez unidades. ¿Cuenta minuciosamente cada unidad una por una, cada vez? ¿O ve rápida y automáticamente un grupo de diez y pide hacer un canje por una barra? Esta simple observación revela la profundidad de su comprensión de la unitización y el valor posicional de manera mucho más efectiva que una prueba escrita. El juego, por lo tanto, no es solo una herramienta para la práctica; es una poderosa herramienta de diagnóstico disfrazada de diversión. Permite a un adulto ver lo que el niño realmente entiende, dónde radican sus fortalezas y qué conceptos podrían necesitar más apoyo, todo dentro de un contexto alegre y alentador.
Concepciones Erróneas Comunes
Cuando un niño comete un error matemático, es tentador simplemente corregir la respuesta y seguir adelante. Sin embargo, un enfoque más efectivo es ver estos errores como valiosas ventanas al pensamiento del niño. Las concepciones erróneas rara vez son aleatorias; a menudo son el resultado de que un niño aplica de manera lógica pero incorrecta una regla que ha aprendido previamente (ASCD Professional Development Online, 2024). El objetivo no es solo “corregir” el error, sino comprender y reconstruir suavemente la lógica defectuosa detrás de él (Institute of Education Sciences, 2024). Esta sección equipa a un adulto para actuar como un “detective de matemáticas”, identificando la causa raíz de los errores comunes de primer grado y utilizando estrategias específicas basadas en bloques para guiar al niño hacia una comprensión más sólida.
Errores como Oportunidades
Crear un entorno de aprendizaje donde los errores se vean como oportunidades para el descubrimiento es primordial (American Psychological Association, 2024). Cuando un niño ofrece una respuesta incorrecta, una respuesta como “Esa es una forma interesante de pensar, vamos a construirlo con los bloques y ver qué pasa” es mucho más productiva que “No, eso está mal”. Este enfoque anima al niño a articular su pensamiento, permitiendo al adulto identificar la concepción errónea específica en juego. Los bloques de base 10 sirven como un árbitro neutral de la verdad; permiten que el niño pruebe su propia hipótesis y descubra el concepto correcto por sí mismo.
Diagnóstico y Corrección
La siguiente tabla describe algunas de las concepciones erróneas más comunes que se encuentran en primer grado, el proceso de pensamiento que probablemente las causa, y preguntas y actividades específicas para abordarlas utilizando bloques de base 10.
| Lo que Ves (La Acción del Niño) | La Concepción Errónea (Proceso de Pensamiento Subyacente) | Pregunta de Sondeo | Actividad Correctiva Específica |
|---|---|---|---|
| Cuenta una colección de 1 barra y 4 unidades como “5”. | Falta de Unitización: El niño ve todos los bloques como “unidades” individuales, independientemente de su tamaño o valor. Aún no ha comprendido que una barra es un solo grupo de diez (Starr, 2023). | “Esta es una barra, pero ¿de cuántas unidades pequeñas está hecha? Vamos a alinear algunas unidades a su lado y ver si coinciden.” | Practica la actividad “Muéstrame 10”. Haz que el niño cuente repetidamente 10 unidades individuales y luego las canjee por una sola barra, diciendo “10 unidades es lo mismo que 1 decena” (Milwaukee Public Schools, 2024). |
| Al resolver 42 - 18, resta 2 de 8 para obtener 6 en la posición de las unidades, resultando en una respuesta de 26. | “La Resta es Conmutativa”: El niño cree que el orden de la resta no importa y que siempre se puede restar el dígito más pequeño del más grande, independientemente de su posición en el problema (ASCD Professional Development Online, 2024). | “Vamos a construir 42 con nuestros bloques. El problema dice que necesitamos quitar 8 unidades. ¿Tenemos suficientes unidades aquí para quitar 8?” (Demuestra físicamente la imposibilidad). | Construye 42 con bloques. Dale al niño el problema en papel y pídele que realice la acción. La imposibilidad física de quitar 8 unidades de 2 creará la necesidad de un “canje hacia abajo”, demostrando por qué el algoritmo funciona de esa manera (Mighty Owl, 2024). |
| Insiste en que el número 52 solo puede mostrarse con 5 barras y 2 unidades. | Valor Posicional Inflexible: El niño ha aprendido la representación estándar de un número pero la ve como la única forma correcta. Carece de una comprensión flexible de la composición de los números (Milwaukee Public Schools, 2024). | “¿Me pregunto si podríamos construir 52 de otra manera? ¿Qué pasaría si canjeáramos una de estas barras por 10 unidades? ¿El valor seguiría siendo 52?” | Juega al juego “¿De Cuántas Maneras?”. Desafía al niño a encontrar tantas combinaciones de bloques diferentes como sea posible para un solo número (por ejemplo, 52, 4 decenas y 12 unidades, 3 decenas y 22 unidades, etc.). Celebra cada representación nueva y correcta que descubra (Third Space Learning, 2024). |
| Al sumar 28 + 34, calcula correctamente 8 + 4 = 12, pero luego escribe la respuesta final como 312. | Malentendido del Algoritmo de Reagrupación: El niño conoce la operación de suma pero no comprende las implicaciones del valor posicional del resultado. Trata el “1” en 12 como una unidad, no como una decena, y escribe el “12” completo en la columna de las unidades, o coloca el 1 en la columna de las centenas (ASCD Professional Development Online, 2024). | “¡Hiciste 12 unidades! ¡Eso es genial! Pero, ¿recuerdas la ‘Regla del Canje’ para la Casa de las Unidades? ¿Qué tenemos que hacer cuando tenemos más de 9 unidades?” | Usa un tapete de valor posicional y realiza físicamente el “Canje hacia Arriba”. Después de canjear 10 unidades por una barra, mueve explícita y dramáticamente la nueva barra a la columna de las decenas, demostrando que su valor pertenece a las otras decenas (ASCD Professional Development Online, 2024). |
Lógica del Error
Los errores matemáticos de un niño rara vez nacen del descuido. A menudo son el resultado lógico de un modelo mental incompleto o sobregeneralizado de cómo funcionan los números. El ejemplo de un niño que “invierte” los dígitos en la resta (42 - 18 se convierte en 42 - 81 en su cabeza) es un caso de estudio perfecto (ASCD Professional Development Online, 2024). El niño está aplicando diligentemente una regla que es cierta en muchos contextos: “restar el más pequeño del más grande”. Aún no ha aprendido las restricciones específicas de esta regla dentro de la estructura del algoritmo formal de la resta.
Reconocer la lógica detrás de su error permite a un adulto tener una conversación más efectiva y validadora. En lugar de decir, “Eso está mal”, se puede decir, “Ya veo lo que hiciste. Sabes que siempre quitamos el número más pequeño del más grande. ¡Eso es inteligente! Pero en este tipo de problema, tenemos que mirar el número entero primero. ¿Es el número entero 42 más grande que el número entero 18?”. Este enfoque valida el razonamiento subyacente del niño mientras corrige suavemente su aplicación. Le ayuda a construir una comprensión más matizada y resistente de las reglas matemáticas al aprender no solo cuáles son, sino también cuándo y por qué se aplican.
Más Allá de los Bloques
Los bloques de base 10 son una herramienta increíblemente poderosa para construir una comprensión fundamental, pero no son el objetivo final. Como los andamios en un edificio, son esenciales para la construcción inicial pero están diseñados para ser retirados una vez que la estructura es sólida (The Institute for Arts Integration, 2024). El objetivo final es que el niño desarrolle un modelo conceptual tan fuerte del sistema numérico que eventualmente pueda resolver problemas de manera abstracta, visualizando los bloques y sus relaciones en su mente. Esta sección final proporciona una hoja de ruta clara para gestionar esta transición crucial del aprendizaje práctico a la competencia matemática duradera.
Tres Etapas de Comprensión
El camino más efectivo para aprender nuevos conceptos matemáticos sigue una progresión de tres etapas conocida como el modelo Concreto-Pictórico-Abstracto (CPA) (Techie Turtle Teacher, 2024). Este marco proporciona una estructura guía para toda la instrucción, capacitando a un adulto para saber en qué punto de su viaje de aprendizaje se encuentra un niño y cuál es el siguiente paso lógico.
Concreto: Esta es la etapa práctica donde el niño manipula físicamente los bloques de base 10 para construir números y resolver problemas. Todas las actividades descritas en las secciones anteriores caen en esta categoría. El dominio en esta etapa es esencial antes de continuar.
Pictórico: En esta etapa, el niño pasa de los objetos físicos a las representaciones visuales. Aprende a dibujar los bloques para resolver problemas en papel.
Abstracto: Esta es la etapa final, donde el niño puede usar numerales y símbolos estándar (por ejemplo, 28 + 34 = 62) para resolver problemas sin la ayuda de bloques o dibujos, porque ha internalizado completamente los conceptos.
El Puente Pictórico
La etapa pictórica no es un paso opcional; es el puente esencial que conecta la comprensión concreta con el razonamiento abstracto. Pasar directamente de los bloques a los algoritmos puede dejar al niño sin una forma de visualizar el proceso, lo que le hace recurrir a la memorización. Esta etapa en sí tiene una progresión de dos pasos:
Dibujos Detallados: Inicialmente, el niño debe dibujar los bloques de una manera que se parezca a los objetos reales: dibujando pequeños cuadrados para las unidades y rectángulos largos para las barras. Esto mantiene un vínculo muy directo con sus experiencias concretas (Techie Turtle Teacher, 2024).
Dibujos Abreviados (“Cuadrados, Palos y Puntos”): A medida que se vuelven más competentes, pueden adoptar un método abreviado más eficiente: dibujar pequeños cuadrados o puntos para las unidades, y líneas rectas o “palos” para las decenas (Techie Turtle Teacher, 2024). Este método abreviado es un paso intermedio vital. Es más rápido y más abstracto que los dibujos detallados, pero aún mantiene la clara representación visual de los grupos de valor posicional. Es una herramienta poderosa para “pensar en papel” y es el precursor directo para comprender el algoritmo abstracto.
Conectando con Algoritmos
Este es el momento culminante donde todo el trabajo práctico se vincula explícitamente con el algoritmo escrito tradicional. Esta conexión debe hacerse a través de una instrucción directa y paralela, mostrando cómo los símbolos en el papel son simplemente un registro de las acciones realizadas con los bloques.
Conectando la Suma: Después de resolver 28 + 34 con bloques y realizar el “Canje hacia Arriba”, coloca el algoritmo escrito junto al tapete. Di: “¿Ves cómo canjeamos 10 de nuestras unidades por una nueva barra y la movimos a la columna de las decenas? Eso es exactamente lo que hacemos en el papel cuando ‘nos llevamos 1’ y lo escribimos encima de la posición de las decenas. ¡Ese pequeño ‘1’ es nuestra nueva barra!” (The Institute for Arts Integration, 2024).
Conectando la Resta: Después de resolver 42 - 15 con bloques y realizar el “Canje hacia Abajo”, muestra el paralelo en el papel. Di: “¿Recuerdas cómo tuvimos que canjear una de nuestras barras por 10 unidades nuevas? Cuando tachamos el 4 y escribimos un 3 encima, y luego escribimos un pequeño ‘1’ junto al 2 para convertirlo en 12, solo estamos dibujando una imagen de lo que hicimos con nuestros bloques. Estamos mostrando que ahora tenemos 3 decenas y 12 unidades.”
Visualización Interna
El propósito de todo este proceso —desde construir y jugar hasta dibujar y conectar— es construir un modelo mental robusto y duradero del sistema numérico. El objetivo no es que un niño necesite los bloques de base 10 para siempre. El objetivo es que sus experiencias con los bloques estén tan profundamente arraigadas que se conviertan en una parte permanente de su pensamiento matemático.
El éxito se logra cuando el niño puede mirar el problema abstracto 52 - 17 en una hoja de papel y, sin ninguna ayuda física, puede visualizar las 5 barras y 2 unidades en su mente. Puede realizar mentalmente el canje, viendo una barra desarmarse en 10 unidades para crear 4 barras y 12 unidades, y luego completar la resta sin esfuerzo. Esta capacidad de ver los números, de manipularlos mentalmente, es el sello distintivo del verdadero sentido numérico. Los bloques, habiendo cumplido su propósito, pueden guardarse, dejando atrás a un joven matemático seguro y capaz.
Bibliografía
- Starr, J. (2023). 3 Signs They Are Ready for Base Ten Blocks (or not!). https://jillianstarrteaching.com/ready-for-base-ten-blocks/
- White Rose Education. (2024). What are Dienes and how to teach using them. https://whiteroseeducation.com/latest-news/what-are-dienes-teach-using-them
- Hand2mind. (2024). How to Use Base Ten Blocks. https://www.hand2mind.com/blog/how-to-use-base-ten-blocks
- Good Neighbors Math. (2024). Understanding Place Value with Base Ten Blocks in the Primary Grades. https://goodneighborsmath.com/understanding-place-value-with-base-ten-blocks-in-the-primary-grades/
- Anthony, S. C. (2024). Teaching Math with Base 10 Blocks. https://www.susancanthony.com/res/tchr/b10.html
- Third Space Learning. (2024). What Are Base Ten Blocks? Explained For Elementary Schools. https://thirdspacelearning.com/us/blog/what-are-base-ten-blocks/
- Math Transformations. (2024). Close to Fifty! Developing Base Ten Concepts and Place Value with First Graders. https://mathtransformations.com/close-to-fifty-developing-base-ten-concepts-and-place-value-with-first-graders/
- Happy Numbers. (2024). Teacher’s Best Friend: Base-10 Blocks. https://happynumbers.com/blog/teachers-best-friend-base-10-blocks/
- Milwaukee Public Schools. (2024). Standard - 1.NBT.2a. https://mps.milwaukee.k12.wi.us/MPS-English/CAO/Documents/RtI-Academics/math-intervention-1NBT2a_ShowMe10.pdf
- Gray, S. (2024). Three Base Ten Activities to Introduce Place Value. https://shelleygrayteaching.com/three-base-ten-activities-to-introduce-place-value/
- Mighty Owl. (2024). Two-digit subtraction with regrouping. https://www.mightyowl.com/units/two-digit-subtraction-with-regrouping
- Saddle Up for 2nd Grade. (2024). Free Addition with Regrouping Lesson Plan Using Base Ten Blocks. https://saddleupfor2ndgrade.com/free-addition-with-regrouping-lesson-plan/
- Techie Turtle Teacher. (2024). 3-Digit Addition with Regrouping Using Base Ten Blocks. https://techieturtleteacher.com/adding-3-digit-numbers-with-regrouping/
- ASCD Professional Development Online. (2024). Numbers and Operations in Base 10 and Numbers and Operations–Fractions. https://pdo.ascd.org/lmscourses/pd11oc129/media/ccss_math_k-5_m05_reading_nbt-fractionsii.pdf
- The Institute for Arts Integration. (2024). Base Ten Buildings STEAM Activity. https://artsintegration.com/base-ten-buildings-steam-activity/
- ActiLearn. (2024). Base Ten Blocks Activities: Fun Games for Place Value. https://actilearnplay.com/base-ten-blocks-activities/
- Institute of Education Sciences. (2024). Assisting Students Struggling with Mathematics-Elementary Intervention: Practice Guide Summary. https://ies.ed.gov/ncee/wwc/Docs/PracticeGuide/WWC-PraxGuide-Elementary-Math-Summary-508c.pdf
- Third Space Learning. (2024). The 4-Stage Process To Fixing Maths Misconceptions. https://thirdspacelearning.com/blog/addressing-misconceptions-process/
- American Psychological Association. (2024). How do I get my students over their alternative conceptions (misconceptions) for learning. https://www.apa.org/education-career/k12/misconceptions
- Mr. T-Rex’s 5th Grade Class Page. (2024). Common Misconceptions Intervention Strategies. https://mr-trex.weebly.com/uploads/3/9/9/5/39956389/use_place_value_strategies_to_add_and_subtract_whole_numbers___grade_4_unit_3__table__3_.pdf




