
Índice de Contenidos
Límites
Definición
Sea \(f\) una función. Se dice que el límite de \(f\) cuando \(x\) tiene a un valor \(a\) es \(L\) si para “acercar” el valor de \(f(x)\) a \(L\) tanto como se quiera basta con “acercar suficientemente” \(x\) al valor \(a\) y se denota como:
\[\begin{equation} \label{eq:limit0} \lim_{x \to a} f(x) = L \end{equation}\]Un Juego de Límites
Vamos a jugar un juego que nos ayudará a comprender este concepto un poco mejor. El juego funciona de la siguiete manera. Tu movida consiste en escoger un intervalo en el eje \(y\) con \(L\) en el centro. Puedes dibujar rectas paralelas al eje \(x\) que pasan por los extremos de tu intervalo. A continuación un ejemplo de como podría lucir tu movida.
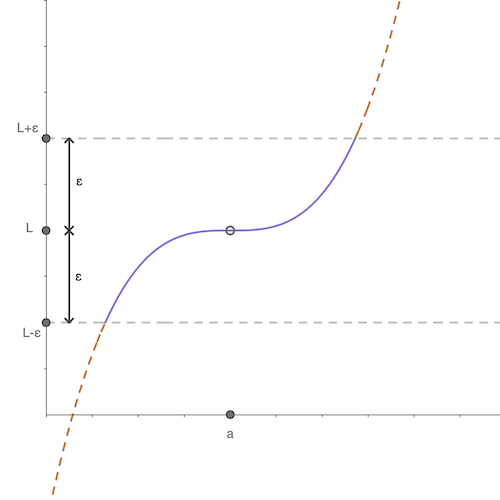
Nota como he etiquetado los extremos del intervalo como \(L-\varepsilon\) y \(L+\varepsilon\). Así que ambos extremos están a una distancia \(\varepsilon\) de \(L\).
En fin, el punto es que no estás dispuesto a tolerar que ninguna parte de la función se pase de esas dos rectas horizontales.
Por otro lado, mi movida consiste en descartar una parte de la función por medio de restringir su dominio. Tan solo me tengo que asegurar de que el nuevo dominio sea un intervalo con \(a\) como su centro y que cada parte de la función resultante quede dentro de las dos rectas que definiste, excepto posiblemente en \(x=a\). Por ejemplo, mi movida podría lucir de la siguiente manera:
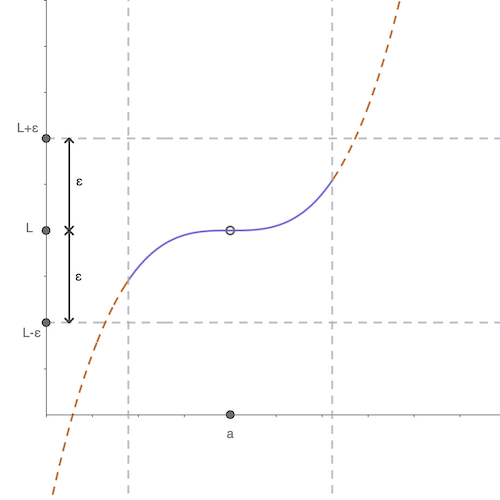
Podría incluso haber descartado más y eso estaría bien, siempre y cuando lo que queda esté dentro de las dos rectas que definiste en tu movida.
Ahora es tu turno de nuevo. Ya te habrás dado cuenta de que mi trabajo se vuelve más complicado a medida que tus dos rectas se acercan la una a la otra, así que esta vez escoges un valor \(\varepsilon\) mucho más pequeño.
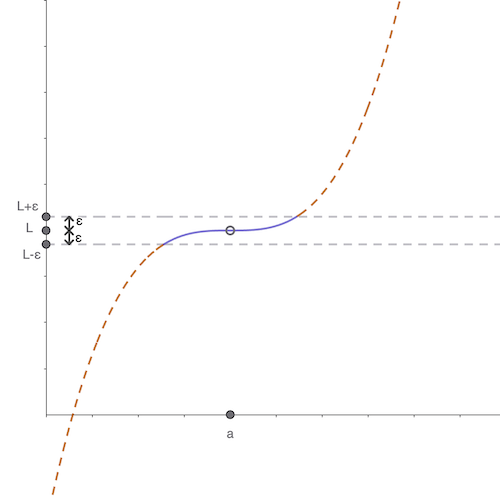
Una buena parte de la curva quedó por fuera de las rectas horizontales que definiste. Esta vez, en mi movida voy a descarcar aún más del dominio de la función alrededor de \(x=a\).
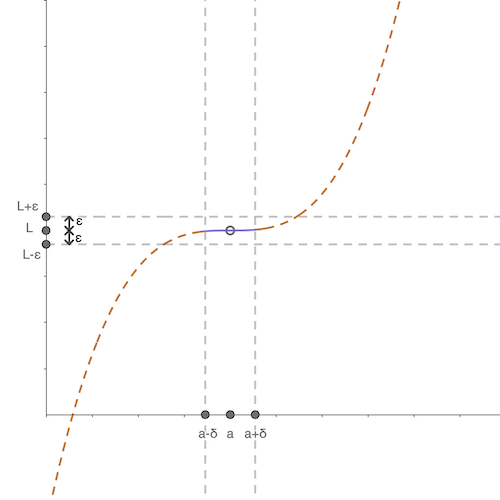
Así que, una vez más, he podido hacer una movida para contrarrestar la tuya.
¿Cuándo se termina este juego? La respuesta es que posiblemente nunca. Si es verdad que yo siempre me puedo mover, sin importar que tan cercanas hagas tus dos rectas, entonces es verdad que:
\[\lim_{x \to a} f(x) = L\]Ambos nos acercaríamos cada vez más. Tu empujado tus dos rectas cada vez más cerca. Yo respondería con partes de la función que están cada vez más cerca a \(x=a\). Si por alguna razón llegara a suceder que ya no puedo hacer otra movida, entonces no es verdad que \(\displaystyle \lim_{x \to a} f(x) = L\). El límite podría ser otro, o podría no existir, pero definitivamente no sería \(L\).
En este juego, “\(\displaystyle \lim_{x \to a} f(x) = L\)” significa que para cualquier elección que hagas de un \(\varepsilon > 0\), yo puedo encontrar un \(\delta>0\) tal que \(\lvert f(x)-L \rvert < \varepsilon\) para todo \(x\) que satisface que \(0 < \lvert x-a \rvert < \delta\).
Es fundamental que mi movida ocurra después de la tuya, pues mi elección de un \(\delta\) depende de tu elección de un \(\varepsilon\). Normalmente no es posible elegir un \(\delta\) que pueda satisfacer cualquier \(\varepsilon > 0\). Por eso, yo siempre debo adaptarme a tu elección.
Exploración Alegórica Alternativa
Supongamos que queremos que \(f(x)\) se aproxime a \(L\) lo más cerca posible dentro de un margen de error o tolerancia \(\varepsilon >0\). Entonces decimos que:
\[\begin{align} \begin{split} f(x) \in \; ]L-\varepsilon,L+\varepsilon[ \\ L-\varepsilon < f(x) < L+\varepsilon \\ -\varepsilon < f(x)-L < \varepsilon \\ |f(x)-L| < \varepsilon \end{split} \end{align}\]Podemos ver claramente que esa última expresión se puede leer como que la distancia entre \(f(x)\) y \(L\) es inferior al margen de error \(\varepsilon\).
Para ilustrarlo, imagina que eres un arquero y que debes colocar una flecha en un blanco (\(L\)), pero dentro de un radio de margen de error (\(\varepsilon\)): un círculo rojo alrededor del punto central. Tu eres la \(x\) y tu reto como arquero experimentado es ubicarte a una distancia muy cercana del punto de disparo (\(a\)), pero sin llegar a pararte directamente en él, que garantice que darás en el blanco. Siempre estarás a un radio de distancia (\(\delta\)) del punto de disparo \(a\) antes de lanzar tu flecha. Tu flecha, bien podría dar exactamente en el punto central \(L\), pero también podría caer muy cerca del mismo. La cosa es que siempre y cuando tu flecha caiga dentro del radio del margen de error (\(\varepsilon\)), se dice que has dado en blanco (\(L\)). Es decir, se cumple que \(\displaystyle \lim_{x \to a} f(x) = L\).
Exploremos la definición en detalle: sea un \(\varepsilon>0\) cualquiera, y supongamos la existencia de un \(\delta >0\) que define un intervalo dentro del cual \(x\) se aproxima a \(a\) (pero sin llegar a alcanzarlo, i.e. \(x \neq a\)). A medida que \(x\) se aproxima arbitrariamente a \(a\) se cumple que \(f(x)\) se aproxima a \(L\) dentro del margen de error \(\varepsilon > 0\) preestablecido como aceptable.
Luego, el intervalo de movimiento de \(x\) se puede denotar de la siguiente manera:
\[x \in \; ]a-\delta,a[ \; \cup \; ]a,a+\delta[\]O alternativamente:
\[x \in \; ]a-\delta,a+\delta[ - \{a\}\]Esto también se podría expresar como:
\[\begin{align} \begin{split} a-\delta < x < a+\delta &\;\; \land \;\; x \neq a \\ -\delta < x-a < \delta &\;\; \land \;\; x-a \neq 0 \\ 0 < |x-a| < \delta \end{split} \end{align}\]Recordemos que el objetivo es encontrar un intervalo de esta forma de tal suerte que toda \(x\) en este intervalo, le permite a \(f(x)\) atinarle al objetivo \(L\) dentro de un margen de error (\(\varepsilon\)).
Así pues, el límite en \(\eqref{eq:limit0}\) se puede definir formalmente como:
\[\begin{equation} \forall{\varepsilon > 0}, \exists{\delta>0}: 0 < |x-a| < \delta \implies |f(x)-L| < \varepsilon \end{equation}\]Demostraciones
En los ejercicios de demostración vamos a emplear la definición de límite para demostrar que el límite es válido.
\[\lim_{x \to a} f(x) = L\]Usando su definición:
\[\begin{equation} \forall{\varepsilon>0},\exists{\delta>0}: 0 < |x-a| < \delta \implies |f(x)-L| < \varepsilon \end{equation}\]Continuando con la analogía del arquero:
- El reto (\(\varepsilon\)): Alguien pinta un círculo rojo alrededor del centro del blanco (\(L\)). Ese círculo tiene radio \(\varepsilon\). Cuanto más pequeño el círculo, más difícil el reto.
- Tu respuesta (\(\delta\)): Tú debes definir un “círculo de seguridad” en el suelo alrededor de tu posición de tiro ideal (\(a\)). Ese círculo tiene radio \(\delta\).
- La garantía (demostración): Demostrar el límite significa probar que, si te paras en cualquier punto dentro de tu círculo de seguridad en el suelo (\(0 < \lvert x-a \rvert < \delta\)), tu flecha obligatoriamente caerá dentro del círculo rojo del blanco (\(\lvert f(x)-L \rvert < \varepsilon\)).
Repaso de Propiedades
Al analizar los siguientes ejemplos de demostraciones, ten presentes las siguientes propiedades:
| 1. Valor Absoluto: | \(\lvert x \rvert = \begin{cases}x &, \text{si $x\geq0$} \\ -x &, \text{si $x<0$}\end{cases}\) |
| 2. Producto del Valor Absoluto | \(\lvert a \cdot b \rvert = \lvert a\rvert \cdot \lvert b \rvert\) |
| 3. Simetría del Valor Absoluto | \(\lvert a - b \rvert = \lvert b - a\rvert\) |
| 4. Desigualdad Triangular | \(\lvert x-a \rvert < b \iff -b < x-a < b\) |
| 5. Desigualdad del Recíproco: | \(a<b \implies\frac{1}{a} > \frac{1}{b}\) siempre que \(a>0 \land b> 0\) |
| 6. Transitividad de la Desigualdad | \(a < b \leq c \implies a < c\) |
Ejemplo 1
Demuestre, usando la definición de límite, que:
\[\begin{equation} \label{lim:ej01} \lim_{x \to -3} (2x-4) = -10 \end{equation}\]Definición del Enunciado
Para todo \(\varepsilon>0\) existe un \(\delta>0\) tal que
\[\begin{equation} 0< |x - (-3)| < \delta \implies |(2x-4)-(-10)| < \varepsilon \end{equation}\]Simplificando:
\[\begin{equation} \label{lim:def1} \boxed{0< |x + 3| < \delta \implies |2x+6| < \varepsilon} \end{equation}\]Simplificar la Tesis
\[\begin{align} \begin{split} |2x+6| < \varepsilon \\ |2(x+3)| < \varepsilon \\ |2|\,|x+3| < \varepsilon \\ 2\,|x+3| < \varepsilon \\ \boxed{|x+3| < \frac{\varepsilon}{2}} \end{split} \end{align}\]Encontrar \(\delta\)
- Por hipótesis, \(0< \lvert x + 3 \rvert < \delta\)
- Por tesis, \(\lvert x+3 \rvert < \frac{\varepsilon}{2}\)
Entonces, se puede concluir que:
\[\begin{equation} \label{lim:delta01} \boxed{0 < \lvert x + 3 \rvert < \delta \leq \frac{\varepsilon}{2}} \end{equation}\]Demostración Sintético-Constructiva
Sea \(\varepsilon>0\), tomando \(\delta = \frac{\varepsilon}{2}\) y suponiendo que \(0< \lvert x + 3 \rvert < \delta\).
\[\begin{align} \begin{split} |x + 3| < \delta &\quad \text{[Por hipótesis \eqref{lim:def1}]}\\ 2\,|x + 3| < 2\delta &\quad \text{[Mult. por 2]}\\ |2x + 6| < 2\delta &\quad \text{[Distribuye 2]} \\ |2x + 6| < 2 \cdot \frac{\varepsilon}{2} &\quad \text{[Por $\eqref{lim:delta01}$]} \\ \boxed{|2x + 6| < \varepsilon} & \end{split} \end{align}\]Por lo tanto, para todo \(\varepsilon > 0\) existe un \(\delta > 0\), tal que \(0 < \lvert x + 3 \rvert < \delta \implies \lvert 2x+6 \rvert < \varepsilon\).
Luego, el límite \(\eqref{lim:ej01}\) queda demostrado.
Demostración Analítico-Transitiva
Existen un segundo estilo de hacer la demostración:
Sea \(\varepsilon>0\) y tomando \(\delta = \frac{\varepsilon}{2}\), supongamos que \(0< \lvert x + 3 \rvert < \delta\).
Entonces se cumple que:
\[\begin{align*} |f(x)-L| &= |2x + 6| &\quad \text{[Por tesis \eqref{lim:ej01}]} \\ &= 2|x+3| & \\ &< 2\delta & \quad \text{[Por hipótesis \eqref{lim:ej01}]} \\ &\leq 2 \cdot \frac{\varepsilon}{2} &\quad \text{[Por $\eqref{lim:delta01}$]} \\ &=\varepsilon \end{align*}\]Luego, si \(\vert 2x+6 \rvert < 2\delta \leq \varepsilon\), por transitividad \(\vert 2x+6 \rvert < \varepsilon\).
Por lo tanto, para todo \(\varepsilon > 0\) existe un \(\delta > 0\), tal que \(0 < \lvert x + 3 \rvert < \delta \implies \lvert 2x+6 \rvert < \varepsilon\).
Luego, el límite \(\eqref{lim:ej01}\) queda demostrado.
Ejemplo 2
Puede resultar interesante demostrar, por definición, que el límite de una función afín es el siguiente:
\[\begin{equation} \label{lim:ej02} \lim_{x \to a} mx + b = ma +b \end{equation}\]Definición del Enunciado
El enunciado dice que, dado un \(\varepsilon > 0\), existe un \(\delta>0\), tal que:
\[\begin{equation} \label{lim:def2} 0< |x-a| < \delta \implies |mx+b-(ma+b)|< \varepsilon \end{equation}\]Simplificar Tesis
\[\begin{align} \begin{split} |mx+b-(ma+b)|< \varepsilon \\ |mx+b-ma-b|< \varepsilon \\ |mx-ma|< \varepsilon \\ |m(x-a)|< \varepsilon \\ \boxed{|x-a|< \frac{\varepsilon}{|m|}} \end{split} \end{align}\]Encontrar \(\delta\)
- Por hipótesis \(\lvert x-a \rvert < \delta\)
- Por tesis \(\lvert x-a \rvert < \dfrac{\varepsilon}{\lvert m \rvert}\)
Entonces
\[\begin{equation} \boxed{|x-a| < \delta \leq \frac{\varepsilon}{|m|}} \end{equation}\]Demostración
Sea \(\varepsilon > 0\), tomando \(\delta = \dfrac{\varepsilon}{\vert m \rvert}\), y suponiendo que \(0< \lvert x-a \rvert < \delta\):
\[\begin{align}\begin{split} |m| \cdot |x-a| < |m| \cdot \delta \\[2mm] |m(x-a)| < |m| \cdot \frac{\varepsilon}{|m|} \\[2mm] \boxed{|x-a| < \varepsilon} \end{split}\end{align}\]Luego, por definición, el límite \(\eqref{lim:ej02}\) queda demostrado.
Ejemplo 3
Dado \(f(x)=x^2\), demostrar que
\[\begin{equation} \label{lim:ej03} \lim_{x \to 2} f(x) = 4 \end{equation}\]Definición del Enunciado
El enunciado dice que, dado un \(\varepsilon > 0\), existe un \(\delta>0\), tal que:
\[\begin{equation} \label{lim:def3} \boxed{0< |x-2| < \delta \implies |x^2-4|< \varepsilon} \end{equation}\]Sabemos que:
\[\begin{align} \begin{split} |x^2-4|< \varepsilon &\quad \text{[Tesis a demostrar $\eqref{lim:def3}$]} \\ |(x+2)(x-2)|< \varepsilon &\quad \\ |x+2|\,|x-2|< \varepsilon &\quad \end{split} \end{align}\]Encontrar el Valor \(\delta\):
Por hipótesis \(\eqref{lim:def3}\), sabemos que \(0 < \lvert x-2 \rvert < \delta\). Como \(x \to 2\) es claro que la diferencia de \(\lvert x-2 \rvert\) será arbitrariamente pequeña, entonces podemos acotar \(\lvert x-2 \rvert\) superiormente asumiendo que \(d \leq 1\):
\[\begin{equation} \label{lim:delta3} \boxed{0 < \delta \leq 1} \end{equation}\]Luego:
\[\begin{align} \begin{split} \label{lim:xval3} |x-2| < \delta &\quad \text{[Por hipótesis $\eqref{lim:def3}$]} \\ |x-2| < 1 &\quad \text{[Acotando con $\delta=1$]} \\ -1 < x-2 < 1 &\quad \text{[Desigualdad triangular]} \\ \boxed{1 < x < 3} & \quad \text{[Sumando 2]} \end{split} \end{align}\]Ya habíamos establecido que la tesis \(\eqref{lim:def3}\) a demostrar es:
\[|x+2|\,|x-2|< \varepsilon\]El problema en este caso es \(\lvert x + 2 \rvert\) es un factor no numérico. Al imponer la condicion de que \(\delta \leq 1\) \(\eqref{lim:delta3}\) se implica que para un \(\varepsilon > 0\) se buscará un \(\delta>0\) tal que el intervalo \(]2-\delta,2+\delta[\) esté contenido en el intervalo \(]1,3[\) establecido en \(\eqref{lim:xval3}\). Esto se produce sin pérdida de generalidad, pues la definición de límite lo que establece es la existencia de un \(\delta\). Esta condición impuesta \(\eqref{lim:delta3}\) solo está delimitando el espacio en el cual se hará la búsqueda de dicho valor. Esta condición nos permite acotar superiormente estos factores no numéricos.
Sabiendo que \(x<3\), según \(\eqref{lim:xval3}\), podemos encontrar una cota superior para \(\lvert x+2 \rvert\) de la siguiente manera:
\[\begin{align} \begin{split} \label{lim:cota3x2} 1 < x < 3 & \quad \text{[Por $\eqref{lim:xval3}$]} \\ 3 < x + 2 < 5 \\ \boxed{3 < |x + 2| < 5} \end{split} \end{align}\]Luego, si \(\lvert x + 2 \rvert < 5\), entonces:
\[\begin{align} \begin{split} \label{lim:cota3e} |x+2|\,|x-2| & < 5 \cdot |x-2| < \varepsilon \\ & \implies \boxed{|x-2| < \frac{\varepsilon}{5}} \end{split} \end{align}\]Llegado a este punto, podemos concluir lo siguiente:
- Por hipótesis \(\lvert x-2 \rvert < \delta\), \(\eqref{lim:def3}\)
- Siempre que \(\delta \leq 1\), \(\eqref{lim:delta3}\).
- Se estableció en \(\lvert x-2 \rvert < \frac{\varepsilon}{5}\), \(\eqref{lim:cota3e}\).
Se concluye que:
\[\begin{align} 0 < \delta \leq 1 \land 0 < \delta \leq \frac{\varepsilon}{5} \\ \end{align}\]Se toma la menor cota superior de las dos, usualmente expresado como:
\[\begin{equation} \label{lim:mdelta3} \boxed{0 < \delta \leq min\Biggl\{1,\frac{\varepsilon}{5}\Biggr\}} \end{equation}\]Demostración Sintético-Constructiva
Sea \(\varepsilon > 0\), tomando \(\delta = min\Bigl\{1, \dfrac{\varepsilon}{5}\Bigr\}\), y supongamos que \(0 < \lvert x-2 \rvert < \delta\) entonces:
\[\begin{align} \begin{split} |x-2| &< \delta & \quad \text{[Por hipótesis $\eqref{lim:def3}$]}\\ 5 \cdot |x-2| &< 5 \cdot \delta & \\ |x+2|\;|x-2| &< 5 \cdot |x-2| < 5 \cdot \delta & \quad \text{[Por $\eqref{lim:cota3x2}$]} \\ |x+2|\;|x-2| &< 5 \cdot \delta & \quad \text{[Por transitividad]} \\ |(x+2)(x-2)| &< 5 \cdot \delta & \\ |x^2 - 4| &< 5 \cdot \delta & \\ |x^2 - 4| &< 5 \cdot min\Bigl\{\dfrac{\varepsilon}{5}, 1\Bigr\} & \quad \text{[Reemplaza $\delta$ por $\eqref{lim:mdelta3}$]} \\ |x^2 - 4| &< 5 \cdot \frac{\varepsilon}{5} & \\ |x^2 - 4| &< \varepsilon & \end{split} \end{align}\]Un monento, ¿que pasaría en el caso que escojamos un \(\varepsilon > 5\), por ejemplo, con \(\varepsilon = 6\)?
Bueno, la demostración sigue siendo válida
\[\begin{align*} |x^2 - 4| &< 5 \cdot min\Bigl\{\dfrac{6}{5}, 1\Bigr\} \\ |x^2 - 4| &< 5 \cdot (1) \\ & \implies |x^2 - 4| < \varepsilon & \quad \text{[Pues $\varepsilon=6$]} \end{align*}\]Por lo tanto, para todo \(\varepsilon > 0\), existe un \(\delta > 0\) tal que, \(0< \lvert x-2 \rvert < \delta \implies \lvert x^2-4 \rvert< \varepsilon\).
Luego, por definición, el límite \(\eqref{lim:ej03}\) queda demostrado.
Demostración Analítico-Transitiva
Sea \(\varepsilon > 0\), tomando \(\delta = min\Bigl\{\dfrac{\varepsilon}{5}, 1\Bigr\}\), y supongamos que \(0 < \lvert x-2 \rvert < \delta\) entonces:
\[\begin{align} \begin{split} |f(x)-L| &= |x^2 - 4| & \quad \text{[Por hipótesis $\eqref{lim:def3}$]} \\ &=|(x+2)(x-2)| \\ &<5|x-2| & \quad \text{[Por $\eqref{lim:cota3x2}$]} \\ &<5\delta & \quad \text{[Por hipótesis $\eqref{lim:def3}$]}\\ &\leq 5 \cdot min\Bigl\{\dfrac{\varepsilon}{5}, 1\Bigr\} & \quad \text{[Reemplaza $\delta$ por $\eqref{lim:mdelta3}$]} \\ &\leq 5 \cdot \frac{\varepsilon}{5} \\ &=\varepsilon \end{split} \end{align}\]Luego, si \(\lvert x^2 - 4 \rvert < 5\delta \leq \varepsilon\), por transitividad \(\lvert x^2 - 4 \rvert < \varepsilon\).
Por lo tanto, para todo \(\varepsilon > 0\), existe un \(\delta > 0\) tal que, \(0< \lvert x-2 \rvert < \delta \implies \lvert x^2-4 \rvert< \varepsilon\).
Luego, por definición, el límite \(\eqref{lim:ej03}\) queda demostrado.
Ejemplo 4
Demostrar, usando la definición de límite, que:
\[\begin{equation} \label{lim:ej04} \lim_{x \to 1} \frac{4}{x+2}=\frac{4}{3} \end{equation}\]Definición del Enunciado
El enunciado dice que, para todo \(\varepsilon > 0\), existe un \(\delta>0\), tal que:
\[\begin{equation} 0 < |x-1| < \delta \implies \left|\frac{4}{x+2}-\frac{4}{3}\right| < \varepsilon \end{equation}\]Simplifiquemos la suma de fracciones:
\[\begin{aligned} \left|\frac{12-4(x+2)}{3(x+2)}\right| = \left|\frac{4-4x}{3(x+2)}\right| = \left|\frac{4(1-x)}{3(x+2)}\right| = \frac{4}{3} \cdot \frac{|1-x|}{|x+2|} \end{aligned}\]Entonces el enunciado sería el siguiente:
\[\begin{equation} 0 < |x-1| < \delta \implies \frac{4}{3} \cdot \frac{|1-x|}{|x+2|} < \varepsilon \end{equation}\]Con el fin de aislar \(\lvert x-1 \rvert\), esto se puede expresar alternativamente como:
\[\begin{equation} \label{lim:def4} \boxed{0 < |x-1| < \delta \implies \frac{4}{3} \cdot \frac{1}{|x+2|} \cdot |x-1| < \varepsilon} \end{equation}\]Encontrar el Valor \(\delta\):
Por hipótesis \(\eqref{lim:def4}\), sabemos que \(0 < \lvert x-1 \rvert < \delta\). Como \(x \to 1\) es claro que la diferencia de \(\lvert x-1 \rvert\) será arbitrariamente pequeña, entonces podemos acotar \(\lvert x-1 \rvert\) superiormente asumiendo que \(d \leq 1\):
\[\begin{equation} \label{lim:delta4} \boxed{0 < \delta \leq 1} \end{equation}\]Luego:
\[\begin{align} \begin{split} \label{lim:xval4} |x-1| < \delta &\quad \text{[Por hipótesis $\eqref{lim:def4}$]} \\ |x-1| < 1 &\quad \text{[Acotando $\delta=1$]} \\ -1 < x-1 < 1 & \quad \text{[Desigualdad triangular]} \\ \boxed{0 < x < 2} & \end{split} \end{align}\]El problema en este caso es \(\frac{1}{\lvert x+2 \rvert}\) es un factor no numérico. Al imponer la condicion de que \(\delta \leq 1\) \(\eqref{lim:delta4}\) se implica que para un \(\varepsilon > 0\) se buscará un \(\delta>0\) tal que el intervalo \(]1-\delta,1+\delta[\) esté contenido en el intervalo \(]0,2[\) establecido en \(\eqref{lim:xval4}\). Esto se produce sin pérdida de generalidad, pues la definición de límite lo que establece es la existencia de un \(\delta\). Esta condición impuesta \(\eqref{lim:delta4}\) solo está delimitando el espacio en el cual se hará la búsqueda de dicho valor. Esta condición nos permite acotar superiormente estos factores no numéricos.
Sabiendo que \(x<2\), según \(\eqref{lim:xval4}\), podemos encontrar una cota superior para \(\frac{1}{\lvert x+2 \rvert}\) de la siguiente manera:
\[\begin{align} \begin{split} \label{lim:xcota4} 0 < x < 2 &\quad \text{[Según $\eqref{lim:xval4}$]} \\ 2 < x + 2 < 4 &\quad \text{[Sumando 2]} \\ \frac{1}{2} > \frac{1}{x+2} > \frac{1}{4} &\quad \text{[Aplicando recíproco]} \\[2mm] \boxed{\frac{1}{4} < \frac{1}{x+2} < \frac{1}{2}} &\quad \text{[Reordenando términos]} \end{split} \end{align}\]Luego:
\[\begin{align} \begin{split} |f(x)-L| &= \frac{4}{3} \cdot \frac{1}{|x+2|} \cdot |x-1| & \quad \text{[Tesis $\eqref{lim:def4}$]} \\[2mm] &< \frac{4}{3} \cdot \frac{1}{2} \cdot |x-1| & \quad \text{[Según $\eqref{lim:xcota4}$]} \\[2mm] &= \frac{2}{3} \cdot |x-1| \\[2mm] &< \varepsilon \end{split} \end{align}\]El lector puede comprobar que, por transitivadad:
\[\begin{aligned} \frac{4}{3} \cdot \frac{1}{|x+2|} \cdot |x-1| < \frac{2}{3} \cdot |x-1| &< \varepsilon \\[2mm] \implies \frac{4}{3} \cdot \frac{1}{|x+2|} \cdot |x-1| &< \varepsilon \\[2mm] \iff |f(x) - L| &< \varepsilon \end{aligned}\]Así las cosas, finalmente podemos aislar \(\lvert x-1 \rvert\):
\[\begin{align} \begin{split} \label{lim:cota4e} \frac{2}{3} \cdot |x-1| &< \varepsilon \\[2mm] \boxed{|x-1| < \frac{3}{2} \cdot \varepsilon} \end{split} \end{align}\]Llegado a este punto, podemos concluir lo siguiente:
- Por hipótesis \(\lvert x-1 \rvert < \delta\), \(\eqref{lim:def4}\)
- Siempre que \(\delta \leq 1\), \(\eqref{lim:delta4}\).
- Se estableció en \(\lvert x-1 \rvert < \dfrac{3\varepsilon}{2}\), \(\eqref{lim:cota4e}\).
Se concluye que:
\[\begin{align} 0 < \delta \leq 1 \land 0 < \delta \leq \frac{3\varepsilon}{2} \\ \end{align}\]Se toma la menor cota superior de las dos, usualmente expresado como:
\[\begin{equation} \label{lim:mdelta4} \boxed{0 < \delta \leq min\Biggl\{1,\frac{3\varepsilon}{2}\Biggr\}} \end{equation}\]Demostración Analítico-Transitiva
Sea \(\varepsilon > 0\), tomando \(\delta = min\Bigl\{\dfrac{3\varepsilon}{2}, 1\Bigr\}\), y suponiendo que \(0 < \lvert x-1 \rvert < \delta\) entonces:
\[\begin{aligned} \begin{split} |f(x)-L| &= \frac{4}{3} \cdot \frac{1}{|x+2|} \cdot |x-1| & \quad \text{[Por hipótesis $\eqref{lim:def4}$]} \\ &< \frac{2}{3} \cdot |x-1| & \quad \text{[Por $\eqref{lim:xcota4}$]}\\[2mm] &< \frac{2}{3} \delta \\[2mm] &\leq \frac{2}{3} \cdot min\Biggl\{1,\frac{3\varepsilon}{2}\Biggr\} & \quad \text{[Por $\eqref{lim:mdelta4}$]}\\[2mm] &\leq \frac{2}{3} \cdot \frac{3\varepsilon}{2} \\[2mm] &=\varepsilon \end{split} \end{aligned}\]Luego, si \(\frac{4}{3} \cdot \frac{1}{\lvert x+2 \rvert} \cdot \vert x-1 \rvert < \frac{2}{3}\delta \leq \varepsilon\), por transitividad \(\frac{4}{3} \cdot \frac{1}{\lvert x+2 \rvert} \cdot \vert x-1 \rvert < \varepsilon\).
Por lo tanto, para todo \(\varepsilon > 0\), existe un \(\delta > 0\) tal que, \(0< \lvert x-1 \rvert < \delta \implies \frac{4}{3} \cdot \frac{1}{\lvert x+2 \rvert} \cdot \vert x-1 \rvert < \varepsilon\).
Luego, por definición, el límite \(\eqref{lim:def4}\) queda demostrado.
Demostración Sintético-Constructiva
Sea \(\varepsilon > 0\), tomando \(\delta = min\Bigl\{\dfrac{3\varepsilon}{2}, 1\Bigr\}\), y suponiendo que \(0 < \lvert x-1 \rvert < \delta\) entonces:
\[\begin{aligned} \begin{split} |x-1| &< \delta & \quad \text{[Por hipótesis $\eqref{lim:def4}$]} \\ \frac{4}{3} \cdot \frac{1}{2} \cdot |x-1| &< \frac{2}{3}\delta \\[2mm] \frac{4}{3} \cdot \frac{1}{|x+2|} \cdot |x-1| &< \frac{2}{3}\delta & \quad \text{[Por $\eqref{lim:xcota4}$]} \\[2mm] \frac{4 \cdot |1-x|}{3 \cdot |x+2|} &< \frac{2}{3} \cdot \frac{3}{2}\varepsilon \\[2mm] \frac{4 \cdot |1-x|}{3 \cdot |x+2|} &< \varepsilon \end{split} \end{aligned}\]Por lo tanto, para todo \(\varepsilon > 0\), existe un \(\delta > 0\) tal que, \(0< \lvert x-1 \rvert < \delta \implies \frac{4 \cdot \vert 1-x \rvert}{3 \cdot \lvert x+2 \rvert} < \varepsilon\).
Luego, por definición, el límite \(\eqref{lim:def4}\) queda demostrado.
Ejemplo 5
Demostrar, usando la definición de límite, que:
\[\begin{equation} \label{lim:ej05} \lim_{x \to 1} \frac{\sqrt{x+1}}{x} = \sqrt{2} \end{equation}\]Definición del Enunciado
El enunciado dice que, para todo \(\varepsilon > 0\), existe un \(\delta>0\), tal que:
\[\begin{equation} 0 < |x-1| < \delta \implies \left|\frac{\sqrt{x+1}}{x} - \sqrt{2}\right| < \varepsilon \end{equation}\]Primero simplifiquemos esa resta en la tesis:
\[\begin{aligned} \left|\frac{\sqrt{x+1}}{x} - \sqrt{2}\right| = \frac{\left|\sqrt{x+1}-\sqrt{2}x\right|}{|x|} \cdot \frac{\left|\sqrt{x+1}+\sqrt{2}x\right|}{\left|\sqrt{x+1}+\sqrt{2}x\right|} \\[3mm] =\frac{\left| 1 + x-2x^2 \right|}{\left| x(\sqrt{x+1}+\sqrt{2}x) \right|} = \frac{\left| -(2x+1)(x-1) \right|}{\left| x(\sqrt{x+1}+\sqrt{2}x) \right|} \\[3mm] = \frac{\left|(2x+1)\right| \cdot \left|(x-1) \right|}{\left|x\right| \cdot \left|(\sqrt{x+1}+\sqrt{2}x)\right|} \end{aligned}\]Luego, la definición para este límite se puede representar, convenientemente, de la siguiente manera:
\[\begin{equation} \label{lim:def5} \boxed{0 < |x-1| < \delta \implies \frac{1}{|x|} \cdot \frac{1}{\left|(\sqrt{x+1}+\sqrt{2}x)\right|} \cdot |2x+1| \cdot |x-1| < \varepsilon} \end{equation}\]Encontrar el Valor \(\delta\):
Por hipótesis \(\eqref{lim:def5}\), sabemos que \(0 < \lvert x-1 \rvert < \delta\). Como \(x \to 1\) es claro que la diferencia de \(\lvert x-1 \rvert\) será arbitrariamente pequeña, entonces podemos acotar \(\lvert x-1 \rvert\) superiormente asumiendo que \(d \leq \frac{1}{2}\):
\[\begin{equation} \label{lim:delta5} \boxed{0 < \delta \leq \frac{1}{2}} \end{equation}\]Luego:
\[\begin{align} \begin{split} \label{lim:xval5} |x-1| < \delta &\quad \text{[Por hipótesis $\eqref{lim:def5}$]} \\ |x-1| < \frac{1}{2} &\quad \text{[Acotando $\delta=\frac{1}{2}$]} \\ -\frac{1}{2} < x-1 < \frac{1}{2} & \quad \text{[Desigualdad triangular]} \\ \boxed{\frac{1}{2} < x < \frac{3}{2}} \end{split} \end{align}\]¿Por qué un \(\delta \leq \frac{1}{2}\) y no \(\delta \leq 1\) como hemos hecho en otros ejemplos? Si acotamos con \(\delta=1\), terminaremos con \(0 < x < 2\). Al intentar obtener una cota para \(1/x\) terminaremos con \(\frac{1}{2} < x < \frac{1}{0} \implies \frac{1}{2} < x < \infty\). En \(x=0\) hay una asíntota vertical, por tanto \(1/x\) no tiene una cota superior cuando \(\delta=1\).
Ahora bien, el problema en este caso es \(\frac{1}{\lvert x \rvert}\), \(\frac{1}{\lvert \sqrt{x+1} + \sqrt{2}x \rvert}\) y \(\lvert 2x+1 \rvert\) no son factores numéricos. Al imponer la condicion de que \(\delta \leq \frac{1}{2}\) \(\eqref{lim:delta5}\) se implica que para un \(\varepsilon > 0\) se buscará un \(\delta>0\) tal que el intervalo \(]1-\delta,1+\delta[\) esté contenido en el intervalo \(]\frac{1}{2},\frac{3}{2}[\) establecido en \(\eqref{lim:xval5}\). Esto se produce sin pérdida de generalidad, pues la definición de límite lo que establece es la existencia de un \(\delta\). Esta condición impuesta \(\eqref{lim:delta5}\) solo está delimitando el espacio en el cual se hará la búsqueda de dicho valor. Esta condición nos permite acotar superiormente estos factores no numéricos.
Comencemos con \(\frac{1}{\lvert x \rvert}\):
\[\begin{align} \begin{split} \label{lim:cota5a} \frac{1}{2} < x < \frac{3}{2} &\quad \text{[Por $\eqref{lim:xval5}$]} \\ 2 > \frac{1}{x} > \frac{2}{3} &\quad \text{[Recíproco]} \\ \frac{2}{3} < \frac{1}{x} < 2 &\quad \text{[Reordenar términos]}\\ \boxed{\frac{2}{3} < \frac{1}{|x|} < 2} \end{split} \end{align}\]Seguidamente \(\lvert 2x+1 \rvert\):
\[\begin{align} \begin{split} \label{lim:cota5b} \frac{1}{2} < x < \frac{3}{2} & \quad \text{[Por $\eqref{lim:xval5}$]}\\ 1 < 2x < 3 & \quad \text{[Mult. por 2)]}\\ 2 < 2x + 1 < 4 & \quad \text{[Suma 1]}\\ \boxed{2 < |2x + 1| < 4} \end{split} \end{align}\]Finalmente, para \(\frac{1}{\lvert \sqrt{x+1} + \sqrt{2}x \rvert}\) acotaremos cada término por separado y los sumaremos al final:
\[\begin{align} \begin{split} \label{lim:cota5c} \frac{1}{2} < x < \frac{3}{2} & \quad \text{[Por $\eqref{lim:xval5}$]}\\ \frac{3}{2} < x+1 < \frac{5}{2} & \quad \text{[Suma 1]} \\ \boxed{\frac{\sqrt{3}}{\sqrt{2}} < \sqrt{x+1} < \frac{\sqrt{5}}{\sqrt{2}}} & \quad \text{[Aplica raíz cuadrada]} \end{split} \end{align}\]Y ahora el segundo término:
\[\begin{equation} \begin{split} \label{lim:cota5d} \frac{1}{2} < x < \frac{3}{2} & \quad \text{[Por $\eqref{lim:xval5}$]} \\[2mm] \frac{\sqrt{2}}{2} < \sqrt{2}x < \frac{3\sqrt{2}}{2} \\[2mm] \boxed{\frac{1}{\sqrt{2}} < \sqrt{2}x < \frac{3}{\sqrt{2}}} & \quad \text{[Racionalizar]} \end{split} \end{equation}\]Ahora sumamos ambos:
\[\begin{align} \begin{split} \label{lim:cota5e} \frac{\sqrt{3}+1}{\sqrt{2}} < \sqrt{x+1} + \sqrt{2}x < \frac{\sqrt{5}+3}{\sqrt{2}} & \quad \text{[Suma $\eqref{lim:cota5c}$ y $\eqref{lim:cota5d}$]}\\[3mm] \frac{\sqrt{2}}{\sqrt{3}+1} > \frac{1}{\sqrt{x+1} + \sqrt{2}x} > \frac{\sqrt{2}}{\sqrt{5}+3} & \quad \text{[Recíproco]}\\[3mm] \frac{\sqrt{2}}{\sqrt{5}+3} < \frac{1}{\sqrt{x+1} + \sqrt{2}x} < \frac{\sqrt{2}}{\sqrt{3}+1} & \quad \text{[Reordenar términos]}\\[3mm] \boxed{\frac{\sqrt{2}(3-\sqrt{5})}{4} < \frac{1}{\sqrt{x+1} + \sqrt{2}x} < \frac{\sqrt{2}(\sqrt{3}-1)}{2}} & \quad \text{[Racionalizar]} \end{split} \end{align}\]Finalmente podemos acotar la tesis de la siguiente manera:
\[\begin{align} \begin{split} |f(x)-L| &= \frac{1}{|x|} \cdot \frac{1}{\left|\sqrt{x+1}+\sqrt{2}x\right|} \cdot |(2x+1)| \cdot |x-1| \\[3mm] &< 2 \cdot \frac{\sqrt{2}(\sqrt{3}-1)}{2} \cdot 4 \cdot |x-1| \\[2mm] &= 4(\sqrt{6}-\sqrt{2}) \cdot |x-1| \\[2mm] &< \varepsilon \end{split} \end{align}\]Una vez más, nótese que \(\lvert f(x)-L \rvert < 4(\sqrt{6}-\sqrt{2}) \cdot \lvert x-1 \rvert < \varepsilon \implies \lvert f(x)-L \rvert < \varepsilon\)
Por lo tanto, podemos acotar \(\lvert x-1 \rvert\) de la siguiente manera:
\[\begin{align} \begin{split} \label{lim:cota5f} 4(\sqrt{6}-\sqrt{2}) \cdot |x-1| < \varepsilon \\[2mm] \boxed{|x-1| < \frac{\varepsilon}{4(\sqrt{6}-\sqrt{2})}} \end{split} \end{align}\]Llegado a este punto, podemos concluir lo siguiente:
- Por hipótesis \(\lvert x-1 \rvert < \delta\), \(\eqref{lim:def5}\)
- Siempre que \(\delta \leq \frac{1}{2}\), \(\eqref{lim:delta5}\).
- Se estableció que \(\lvert x-1 \rvert < \frac{\varepsilon}{4(\sqrt{6}-\sqrt{2})}\), \(\eqref{lim:cota5f}\).
Se concluye que:
\[\begin{align} \left(0 < \delta \leq \frac{1}{2}\right) \land \left(0 < \delta \leq \frac{\varepsilon}{4(\sqrt{6}-\sqrt{2})}\right) \end{align}\]Se toma la menor cota superior de las dos, usualmente expresado como:
\[\begin{equation} \label{lim:mdelta5} \boxed{0 < \delta \leq min\Biggl\{\frac{1}{2},\frac{\varepsilon}{4(\sqrt{6}-\sqrt{2})}\Biggr\}} \end{equation}\]Demostración Analítico-Transitiva
Sea \(\varepsilon > 0\), tomando \(\delta = min\left\{\frac{1}{2},\frac{\varepsilon}{4(\sqrt{6}-\sqrt{2})}\right\}\), y suponiendo que \(0 < \lvert x-1 \rvert < \delta\) entonces:
\[\begin{aligned} \begin{split} |f(x)-L| &= \frac{1}{|x|} \cdot \frac{1}{\left|(\sqrt{x+1}+\sqrt{2}x)\right|} \cdot |2x+1| \cdot |x-1| & \quad \text{[Por hipótesis $\eqref{lim:def5}$]} \\[2mm] &< 4(\sqrt{6}-\sqrt{2}) \cdot |x-1| & \quad \text{[Por $\eqref{lim:cota5f}$]} \\[2mm] &< 4(\sqrt{6}-\sqrt{2})\delta & \quad \text{[Por $\eqref{lim:def5}$]} \\[2mm] &\leq 4(\sqrt{6}-\sqrt{2})\left(\frac{\varepsilon}{4(\sqrt{6}-\sqrt{2})}\right) &\quad \text{[Por $\eqref{lim:mdelta5}$]} \\[2mm] &=\varepsilon \end{split} \end{aligned}\]Por lo tanto, para todo \(\varepsilon > 0\), existe un \(\delta > 0\) tal que, \(0< \lvert x-1 \rvert < \delta \implies \lvert \frac{\sqrt{x+1}}{x} - \sqrt{2} \rvert < \varepsilon\).
Luego, por definición, el límite \(\eqref{lim:def5}\) queda demostrado.
Bibliografía Consultada
- Sancho Mora, L. (2016). Cálculo Diferencial. ENUNED.
- Agüero Calvo, E., & Fallas Monge, J. J. (2025). Cálculo en una Variable. Editorial Tecnológico de Costa Rica.
- Banner, A. (2007). The Calculus Lifesaver. Princeton University Press.




